题目内容
5.已知函数f(x)=$\sqrt{3}$sin(ωx+φ)-cos(ωx+φ)(0<φ<π,ω>0)为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为π.(1)求f($\frac{π}{3}$)的值;
(2)将函数y=f(x)的图象向右平移$\frac{π}{6}$个单位长度后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
分析 (1)由条件利用两角和差的正弦公式化简f(x)的解析式,从而求得f($\frac{π}{3}$)的值.
(2)由条件利用函数y=Asin(ωx+φ)的图象变换规律,求得g(x)的解析式,再根据余弦函数的单调性求得g(x)的单调递减区间.
解答 解:(1)f(x)=$\sqrt{3}$sin(ωx+φ)-cos(ωx+φ)=2[$\frac{\sqrt{3}}{2}$sin(ωx+φ)-$\frac{1}{2}$cos(ωx+φ)]=2sin(ωx+φ-$\frac{π}{6}$),
因为f(x)为偶函数,所以φ-$\frac{π}{6}$=$\frac{π}{2}$+kπ,k∈z,
即φ=$\frac{2π}{3}$+kπ,k∈Z.又因为0<φ<π,所以φ=$\frac{2π}{3}$.
所以f(x)=2sin(ωx+$\frac{π}{2}$)=2cosωx.
由题意得$\frac{2π}{ω}$=2π,所以ω=1.
故f(x)=2cosx,因此f($\frac{π}{3}$)=2cos$\frac{π}{3}$=1.
(2)将f(x)的图象向右平移$\frac{π}{6}$个单位长度后,得到y=2cos(x-$\frac{π}{6}$)的图象.
再将所得图象横坐标伸长到原来的4倍,纵坐标不变,得到y=2cos($\frac{1}{4}$x-$\frac{π}{6}$)的图象.
所以g(x)=2cos($\frac{1}{4}$x-$\frac{π}{6}$).
令2kπ≤$\frac{x}{4}$-$\frac{π}{6}$≤2kπ+π(k∈Z),
求得 8kπ+$\frac{2π}{3}$≤x≤8kπ+$\frac{14π}{3}$(k∈Z),
因此g(x)的单调递减区间为[8kπ+$\frac{2π}{3}$,8kπ+$\frac{14π}{3}$](k∈Z).
点评 本题主要考查两角和差的正弦公式,正弦函数的单调性,奇偶性,周期性,函数y=Asin(ωx+φ)的图象变换规律,属于中档题.

| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
| A. | $\frac{13}{36}$ | B. | $\frac{5}{18}$ | C. | $\frac{7}{36}$ | D. | $\frac{5}{36}$ |
| A. | (0,$\frac{π}{6}$] | B. | [$\frac{π}{6}$,$\frac{π}{4}$] | C. | (0,$\frac{π}{3}$] | D. | [$\frac{π}{3}$,$\frac{π}{2}$] |
| A. | 60 | B. | -60 | C. | 30 | D. | -30 |
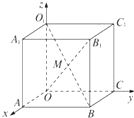 如图所示,在长方体OABC-O1A1B1C1中,|OA|=2,|AB|=3,|AA1|=3,M是OB1与BO1的交点,则M点的坐标是$(1,\frac{3}{2},\frac{3}{2})$.
如图所示,在长方体OABC-O1A1B1C1中,|OA|=2,|AB|=3,|AA1|=3,M是OB1与BO1的交点,则M点的坐标是$(1,\frac{3}{2},\frac{3}{2})$.