题目内容
14.已知$\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}=0$,且|$\overrightarrow{a}$|=3,|$\overrightarrow{b}$|=5,|$\overrightarrow{c}$|=7,则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角是60°.分析 首先利用余弦定理求出以|$\overrightarrow{a}$|,|$\overrightarrow{b}$|,|$\overrightarrow{c}$|为边的三角形内角,然后由向量夹角与三角形内角的关系求出向量夹角.
解答 解:由已知$\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}=0$,且|$\overrightarrow{a}$|=3,|$\overrightarrow{b}$|=5,|$\overrightarrow{c}$|=7
则以|$\overrightarrow{a}$|=BC,|$\overrightarrow{b}$|=AC,|$\overrightarrow{c}$|=AB为边的三角形中cosC=$\frac{{5}^{2}+{3}^{2}-{7}^{2}}{2×5×3}=-\frac{1}{2}$,
所以三角形的内角C=120°,所以向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角是:60°;
故答案为:60°.
点评 本题考查了平面向量的夹角以及余弦定理的运用;关键是明确三个向量围成的三角形内角与向量夹角的关系.

练习册系列答案
相关题目
4.具有线性相关关系的变量x,y,满足一组数据如下表所示:
若y与x的回归直线方程为$\widehat{y}$=3x-$\frac{3}{2}$,则m的值是4.
| X | 0 | 1 | 2 | 3 |
| y | -1 | 1 | m | 8 |
9.下列算法语句的处理功能是( )
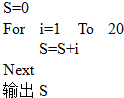
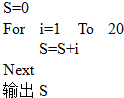
| A. | S=1+2+3+…+20 | B. | S=1+2+3+…+19 | C. | S=2+3+…+20 | D. | S=2+3+…+19 |
3.已知$\vec a$、$\vec b$为两个单位向量,则一定有( )
| A. | $\vec a$=$\vec b$ | B. | $\vec a•\vec b=0$ | C. | $\vec a•\vec b=1$ | D. | $\vec a•\vec a=\vec b•\vec b$ |