题目内容
15.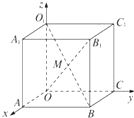 如图所示,在长方体OABC-O1A1B1C1中,|OA|=2,|AB|=3,|AA1|=3,M是OB1与BO1的交点,则M点的坐标是$(1,\frac{3}{2},\frac{3}{2})$.
如图所示,在长方体OABC-O1A1B1C1中,|OA|=2,|AB|=3,|AA1|=3,M是OB1与BO1的交点,则M点的坐标是$(1,\frac{3}{2},\frac{3}{2})$.
分析 结合坐标系正方体的棱长,直接得到M的坐标即可.
解答 解:因为几何体是正方体,在坐标系中,B1点的横坐标是2,纵坐标是2,竖坐标是3,M是点O与B1的中点,
所以M$(1,\frac{3}{2},\frac{3}{2})$.
故答案为:$(1,\frac{3}{2},\frac{3}{2})$.
点评 本题是基础题,考查空间几何体坐标表示,注意判断点的位置.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.若某程序框图如图所示,当输入50时,则该程序运算后输出的结果是( )
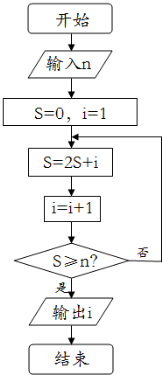

| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
10.复数z满足|z-i|+|z+3|=10,则复数z对应点的集合表示的图形是( )
| A. | 直线 | B. | 圆 | C. | 椭圆 | D. | 双曲线 |
20.已知向量$\overrightarrow{AB}$=(-3,a),$\overrightarrow{AC}$=(1-a,2),若A,B,C三点共线,则a=( )
| A. | 3或-2 | B. | 2或-3 | C. | $\frac{3}{5}$ | D. | 3 |
4.具有线性相关关系的变量x,y,满足一组数据如下表所示:
若y与x的回归直线方程为$\widehat{y}$=3x-$\frac{3}{2}$,则m的值是4.
| X | 0 | 1 | 2 | 3 |
| y | -1 | 1 | m | 8 |
 某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数,按十位数字为茎,个位数字为叶得到的茎叶图如图所示.已知甲、乙两组数据的平均数都为10.
某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数,按十位数字为茎,个位数字为叶得到的茎叶图如图所示.已知甲、乙两组数据的平均数都为10.