题目内容
18.已知f(x)=x2+2,g(x)=sinx,则下列函数中既不是奇函数又不是偶函数的函数是①②(填写所有正确结论对应的序号)①f(x)+g(x);
②f(x)-g(x);
③f(x)•g(x);
④f(g(x));
⑤g(f(x)).
分析 根据函数奇偶性的定义分别进判断即可.
解答 解:f(-x)=x2+2=f(x),则f(x)为偶函数,
g(-x)=-sinx=-g(x),则g(x)为奇函数,
则①f(-x)+g(-x)=f(x)-g(x),则函数为非奇非偶函数;
②f(-x)-g(-x)=f(x)+g(x),则函数为非奇非偶函数;
③f(-x)•g(-x)=-f(x)g(x),则函数为奇函数;
④f(g(-x))=f(-g(x))=f(g(x)),则函数为偶函数;
⑤g(f(-x))=g(f(x))=g(f(x)),则函数为偶函数.
故答案为:①②;
点评 本题主要考查函数奇偶性的判断,根据奇偶性的定义是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.下列函数中,既是偶函数,又在区间(0,+∞)单调递减的是( )
| A. | y=cosx | B. | y=lg|x| | C. | y=-x2+1 | D. | y=x3 |
13.复数$\frac{1+2i}{1+i}$的共轭复数等于( )
| A. | $\frac{1}{2}$+$\frac{1}{2}$i | B. | $\frac{1}{2}$-$\frac{1}{2}$i | C. | $\frac{3}{2}$+$\frac{1}{2}$i | D. | $\frac{3}{2}$-$\frac{1}{2}$i |
4.设F1和F2是双曲线$\left\{\begin{array}{l}x=2secθ\\ y=tanθ\end{array}\right.(θ为$为参数)的两个焦点,点P在双曲线上,且满足∠F1PF2=90°,那么△F1PF2的面积是( )
| A. | 1 | B. | $\frac{{\sqrt{5}}}{2}$ | C. | 2 | D. | 5 |
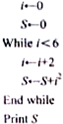 已知某程序伪代码如图,则输出结果S=56.
已知某程序伪代码如图,则输出结果S=56. 已知$\overrightarrow{a}$=(cos$\frac{π}{3}$x,sin$\frac{π}{3}$x),$\overrightarrow{b}$=A(cos2φ,-sin2φ),f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$(A>0,|φ|$<\frac{π}{2}$)的部分图象如图所示,P、Q分别是该图象的最高点和最低点,点P的坐标为(1,A),点R的坐标为(1,0),△PRQ的面积为$\frac{3\sqrt{3}}{2}$.
已知$\overrightarrow{a}$=(cos$\frac{π}{3}$x,sin$\frac{π}{3}$x),$\overrightarrow{b}$=A(cos2φ,-sin2φ),f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$(A>0,|φ|$<\frac{π}{2}$)的部分图象如图所示,P、Q分别是该图象的最高点和最低点,点P的坐标为(1,A),点R的坐标为(1,0),△PRQ的面积为$\frac{3\sqrt{3}}{2}$.