题目内容
14．若x＞0，y＞0且x+2y=xy，则x+2y的最小值为8．分析 由题意可得$\frac{1}{y}$+$\frac{2}{x}$=1，可得x+2y=（x+2y）（$\frac{1}{y}$+$\frac{2}{x}$）=4+$\frac{x}{y}$+$\frac{4y}{x}$，由基本不等式可得．
解答 解：∵x＞0，y＞0且x+2y=xy，
∴$\frac{x+2y}{xy}$=1，即$\frac{1}{y}$+$\frac{2}{x}$=1，
∴x+2y=（x+2y）（$\frac{1}{y}$+$\frac{2}{x}$）
=4+$\frac{x}{y}$+$\frac{4y}{x}$≥4+2$\sqrt{\frac{x}{y}•\frac{4y}{x}}$=8
当且仅当$\frac{x}{y}$=$\frac{4y}{x}$即x=4且y=2时取等号，
故答案为：8
点评 本题考查基本不等式求最值，正确变形是解决问题的关键，属中档题．
练习册系列答案
相关题目
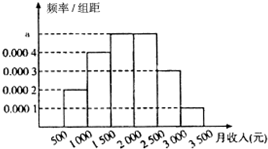统计局就某地居民的月收入情况调查了10000人，并根据所得数据画了样本频率分布直方图，每个分组包括左端点，不包含右端点，如第一组表示收入在[500，1000）．
2．函数f（x）=$\frac{1}{2}$tan2x是（ ）
| A． | 周期为π的偶函数 | B． | 周期为$\frac{π}{2}$的奇函数 | ||
| C． | 周期为$\frac{π}{2}$的偶函数 | D． | 周期为π的奇函数 |
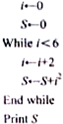已知某程序伪代码如图，则输出结果S=56．
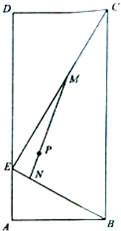某生态农庄池塘的平面图为矩形ABCD，已知AB=4，BC=10，E为AD上一点，且AE=2，P为池塘内一临时停靠点，且P到AB，BC的距离均为3，EC，EB为池塘上浮桥，为了固定浮桥，现准备进过临时停靠点P再架设一座浮桥MN，其中M，N分别是浮桥EC，EB上点．（浮桥宽度、池塘岸边宽度不计），设EM=d，
已知$\overrightarrow{a}$=（cos$\frac{π}{3}$x，sin$\frac{π}{3}$x），$\overrightarrow{b}$=A（cos2φ，-sin2φ），f（x）=$\overrightarrow{a}$•$\overrightarrow{b}$（A＞0，|φ|$＜\frac{π}{2}$）的部分图象如图所示，P、Q分别是该图象的最高点和最低点，点P的坐标为（1，A），点R的坐标为（1，0），△PRQ的面积为$\frac{3\sqrt{3}}{2}$．