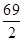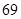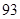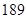题目内容
已知数列{an}的各项均为正数的等比数列,且a1a2=2,a3a4=32,
(1)求数列{an}的通项公式;
(2)设数列{bn}的前n项和为Sn=n2,(n∈N*),求数列{anbn}的前n项和Tn.
(1)求数列{an}的通项公式;
(2)设数列{bn}的前n项和为Sn=n2,(n∈N*),求数列{anbn}的前n项和Tn.
(1)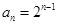 (2)
(2)
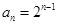 (2)
(2)
试题分析:(1)由已知条件和等比数列的通项公式列出关于q和a1的方程组,解出q和a1即可.
(2)根据bn=Sn-Sn-1,求出数列{bn}的通项公式bn的表达式,然后根据错位相减法求出数列{anbn}的前n项和Tn.
试题解析:(1)设等比数列
 的公比为
的公比为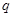 ,由已知得
,由已知得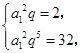 2分
2分又∵
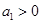 ,
,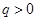 ,解得
,解得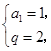 ∴
∴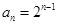 ;
;(2)由
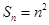 得,
得,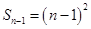 ,
,∴当
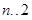 时,
时,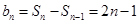 ,当
,当 时,
时,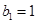 符合上式,∴
符合上式,∴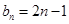 ,(
,(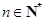 )∴
)∴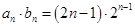 ,
,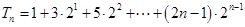 ,
,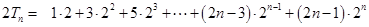 , 10分
, 10分两式相减得
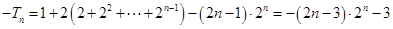 ,
,∴
 . 12分
. 12分
练习册系列答案
相关题目
 ,
,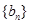 ,
,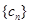 ,已知
,已知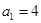 ,
,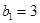 ,
,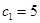 ,
,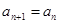 ,
,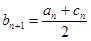 ,
, (
(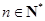 ).
).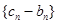 的通项公式;
的通项公式;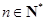 ,
,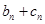 为定值;
为定值;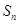 为数列
为数列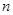 项和,若对任意
项和,若对任意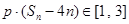 ,求实数
,求实数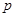 的取值范围.
的取值范围. 改选B菜;而选B菜的,下星期一会有
改选B菜;而选B菜的,下星期一会有 改选A菜。用
改选A菜。用 分别表示第
分别表示第 个星期选A的人数和选B的人数.
个星期选A的人数和选B的人数. 表示
表示 ,判断数列
,判断数列 是否成等比数列并说明理由;
是否成等比数列并说明理由;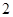 的等比数列
的等比数列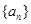 的各项都是正数,且
的各项都是正数,且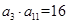 ,则
,则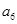 = ( )
= ( )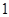
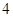
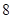
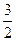 的等比数列{an}不是递减数列, 其前n项和为Sn(n∈N+), 且S3+ a3,S5+ a5,S4+ a4成等差数列,则数列{an}的通项公式为( )
的等比数列{an}不是递减数列, 其前n项和为Sn(n∈N+), 且S3+ a3,S5+ a5,S4+ a4成等差数列,则数列{an}的通项公式为( )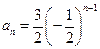
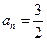
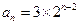 或
或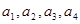 成等比数列,其公比为2,则
成等比数列,其公比为2,则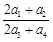 的值为( )
的值为( ) 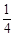
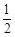
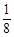
 的通项
的通项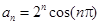 ,则
,则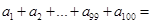 ()
()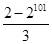
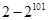
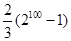
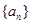 是由正数组成的等比数列,
是由正数组成的等比数列,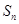 表示
表示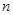 项的和,若
项的和,若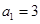 ,
,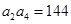 ,则
,则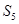 的值是
的值是