题目内容
【题目】已知正方形![]() 的边长为2,分别以
的边长为2,分别以![]() ,
, ![]() 为一边在空间中作正三角形
为一边在空间中作正三角形![]() ,
, ![]() ,延长
,延长![]() 到点
到点![]() ,使
,使![]() ,连接
,连接![]() ,
, ![]() .
.
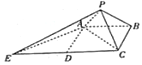
(1)证明: ![]() 平面
平面![]() ;
;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)见解析;(2)1.
【解析】试题分析:(1)证线面垂直,先证线线垂直,做出辅助线,根据长度关系,首先证得![]() ,再证得
,再证得![]() ,
, ![]() ,根据线面垂直的判定定理得到线面垂直;(2)根据条件可得到
,根据线面垂直的判定定理得到线面垂直;(2)根据条件可得到![]() 平面
平面![]() ,进而点
,进而点![]() 到平面
到平面![]() 的距离等于
的距离等于![]() 点到平面
点到平面![]() 的距离,取
的距离,取![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
, ![]() 平面
平面![]() ,
, ![]() 为点
为点![]() 到平面
到平面![]() 的距离.
的距离.
解析:
(1)连接![]() 交
交![]() 于点
于点![]() ,并连接
,并连接![]() ,则
,则![]() ,又∵
,又∵![]() ,
,
∴![]() ,又∵
,又∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() 平面
平面![]() ,∵
,∵![]() 平面
平面![]() ,∴
,∴![]() ,
,
∵![]() ,
, ![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
即![]() ,∵
,∵![]() ,∴
,∴![]() 平面
平面![]() .
.
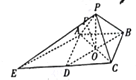
(2)由题知, ![]() ,且
,且![]() ,可得四边形
,可得四边形![]() 为平行四边形,∴
为平行四边形,∴![]() ,
,
又∵![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,∵点
,∵点![]() ,∴点
,∴点![]() 到平面
到平面![]() 的距离等于
的距离等于![]() 点到平面
点到平面![]() 的距离,取
的距离,取![]() 的中点为
的中点为![]() ,连接
,连接![]() ,则由(1)可得
,则由(1)可得![]() .
.
在![]() 中,
中, ![]() ,则
,则![]() ,∴
,∴![]() ,∴
,∴![]() 平面
平面![]() ,即
,即![]() 为点
为点![]() 到平面
到平面![]() 的距离.
的距离.
在![]() 中,
中, ![]() ,得点
,得点![]() 到平面
到平面![]() 的距离为1.
的距离为1.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
【题目】某城市为鼓励人们绿色出行,乘坐地铁,地铁公司决定按照乘客经过地铁站的数量实施分段优惠政策,不超过![]() 站的地铁票价如下表:
站的地铁票价如下表:
乘坐站数 |
|
|
|
票价(元) |
|
|
|
现有甲、乙两位乘客同时从起点乘坐同一辆地铁,已知他们乘坐地铁都不超过![]() 站,且他们各自在每个站下车的可能性是相同的.
站,且他们各自在每个站下车的可能性是相同的.
(1)若甲、乙两人共付费![]() 元,则甲、乙下车方案共有多少种?
元,则甲、乙下车方案共有多少种?
(2)若甲、乙两人共付费![]() 元,求甲比乙先到达目的地的概率.
元,求甲比乙先到达目的地的概率.