题目内容
【题目】【2018广东省深中、华附、省实、广雅四校联考】已知椭圆![]() 的离心率为
的离心率为![]() ,圆
,圆![]() 与
与![]() 轴交于点
轴交于点![]() ,
, ![]() 为椭圆
为椭圆![]() 上的动点,
上的动点, ![]() ,
, ![]() 面积最大值为
面积最大值为![]() .
.
(I)求圆![]() 与椭圆
与椭圆![]() 的方程;
的方程;
(II)圆![]() 的切线
的切线![]() 交椭圆于点
交椭圆于点![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(I)圆![]() 的方程为
的方程为![]() ,椭圆
,椭圆![]() 的方程为
的方程为![]() .(II)
.(II)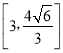
【解析】【试题分析】(1)根据离心率可有![]() ,依题意可知
,依题意可知![]() 为椭圆的焦点,故
为椭圆的焦点,故![]() .当
.当![]() 位于椭圆上顶点时,面积取得最大值,由此列方程可解得
位于椭圆上顶点时,面积取得最大值,由此列方程可解得![]() 的值,并求得圆和椭圆的方程.(2)当直线斜率存在时,设出直线方程为
的值,并求得圆和椭圆的方程.(2)当直线斜率存在时,设出直线方程为![]() ,利用圆和直线相切求得
,利用圆和直线相切求得![]() 的等量关系式,利用韦达定理和弦长公式计算出弦长并利用配方法求得弦长的取值范围.当直线斜率不存在时,直线
的等量关系式,利用韦达定理和弦长公式计算出弦长并利用配方法求得弦长的取值范围.当直线斜率不存在时,直线![]() 的方程为
的方程为![]() ,可直接得到
,可直接得到![]() 的坐标求出弦长.
的坐标求出弦长.
【试题解析】
(1)由题意得![]() ,解得:
,解得: ![]() ①
①
因为![]() ,所以,点
,所以,点![]() 为椭圆的焦点,所以,
为椭圆的焦点,所以, ![]()
设![]() ,则
,则![]() ,所以
,所以![]() ,当
,当![]() 时,
时,
![]() ,代入①解得
,代入①解得![]() ,所以
,所以![]() ,
,
所以,圆![]() 的方程为
的方程为![]() ,椭圆
,椭圆![]() 的方程为
的方程为![]() .
.
(2)①当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,
, ![]()
因为直线![]() 与圆相切,所以
与圆相切,所以![]() ,即
,即![]() ,
,
联立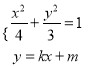 ,消去
,消去![]() 可得
可得![]() ,
,
![]() ,
,
![]()
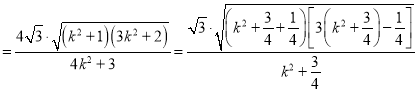
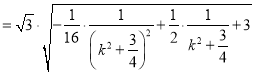
令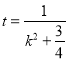 ,则
,则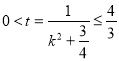 ,所以
,所以![]() ,
,
所以![]() ,所以
,所以![]()
②当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 的方程为
的方程为![]() ,解得
,解得![]() ,
,
综上, ![]() 的取值范围是
的取值范围是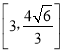 .
.

练习册系列答案
相关题目