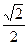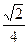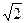题目内容
已知|
|=1,
•
=
,(
-
)•(
+
)=
,求:
(1)
与
的夹角;
(2)
-
与
+
的夹角的余弦值.
| a |
| a |
| b |
| 1 |
| 2 |
| a |
| b |
| a |
| b |
| 1 |
| 2 |
(1)
| a |
| b |
(2)
| a |
| b |
| a |
| b |
(1)∵(
-
)•(
+
)=
,∴
2-
2=
.
又∵|
|=1,∴12-|
|2=
,解得|
|=
.
∵
•
=
,
∴cos<
,
>=
=
=
,
∴
与
的夹角为
;
(2)由(1)可得|
-
|=
=
=
,
|
+
|=
=
=
.
∴cos<
-
,
+
>=
| a |
| b |
| a |
| b |
| 1 |
| 2 |
| a |
| b |
| 1 |
| 2 |
又∵|
| a |
| b |
| 1 |
| 2 |
| b |
| ||
| 2 |
∵
| a |
| b |
| 1 |
| 2 |
∴cos<
| a |
| b |
| ||||
|
|
| ||||
1×
|
| ||
| 2 |
∴
| a |
| b |
| π |
| 4 |
(2)由(1)可得|
| a |
| b |
|
12+(
|
| ||
| 2 |
|
| a |
| b |
|
12+(
|
| ||
| 2 |
∴cos<
| a |
| b |
| a |
| b |
(
| ||||||||
|
|

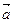 =(3,4),
=(3,4),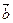 =(sin
=(sin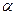 ,cos
,cos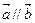 ,则tan
,则tan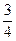
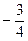
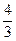
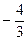
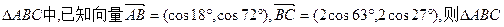 的面积等于
的面积等于