ÌâÄ¿ÄÚÈÝ
ÍÖÔ²G£º
+
=1(a£¾b£¾0)µÄÁ½¸ö½¹µãΪF1£¨-c£¬0£©£¬F2£¨c£¬0£©£¬MÊÇÍÖÔ²ÉϵÄÒ»µã£¬ÇÒÂú×ã
•
=0£®
£¨1£©ÇóÀëÐÄÂʵÄÈ¡Öµ·¶Î§£»
£¨2£©µ±ÀëÐÄÂÊeÈ¡µÃ×îСֵʱ£¬µãN£¨0£¬3£©µ½ÍÖÔ²ÉϵĵãµÄ×îÔ¶¾àÀëΪ5
£»
¢ÙÇó´ËʱÍÖÔ²GµÄ·½³Ì£»
¢ÚÉèбÂÊΪk£¨k¡Ù0£©µÄÖ±ÏßLÓëÍÖÔ²GÏཻÓÚ²»Í¬µÄÁ½µãA¡¢B£¬QΪABµÄÖе㣬ÎÊA¡¢BÁ½µãÄÜ·ñ¹ØÓÚ¹ýµãP(0£¬-
)¡¢QµÄÖ±Ï߶Գƣ¿ÈôÄÜ£¬Çó³ökµÄÈ¡Öµ·¶Î§£»Èô²»ÄÜ£¬Çë˵Ã÷ÀíÓÉ£®
| x2 |
| a2 |
| y2 |
| b2 |
| F1M |
| F2M |
£¨1£©ÇóÀëÐÄÂʵÄÈ¡Öµ·¶Î§£»
£¨2£©µ±ÀëÐÄÂÊeÈ¡µÃ×îСֵʱ£¬µãN£¨0£¬3£©µ½ÍÖÔ²ÉϵĵãµÄ×îÔ¶¾àÀëΪ5
| 2 |
¢ÙÇó´ËʱÍÖÔ²GµÄ·½³Ì£»
¢ÚÉèбÂÊΪk£¨k¡Ù0£©µÄÖ±ÏßLÓëÍÖÔ²GÏཻÓÚ²»Í¬µÄÁ½µãA¡¢B£¬QΪABµÄÖе㣬ÎÊA¡¢BÁ½µãÄÜ·ñ¹ØÓÚ¹ýµãP(0£¬-
| ||
| 3 |
£¨1£©ÉèM£¨x£¬y£©£¬Ôò
=(x+c£¬y)£¬
=(x-c£¬y)
ÓÉ
•
=0⇒x2+y2=c2⇒y2=c2-x2£¨1·Ö£©
ÓÖMÔÚÍÖÔ²ÉÏ£¬¡ày2=b2-
x2£¨2·Ö£©
¡àc2-x2=b2-
x2⇒x2=a2-
£¬£¨3·Ö£©
ÓÖ0¡Üx2¡Üa2¡à0£¼2-
¡Ü1⇒
¡Üe¡Ü1£¬£¨4·Ö£©
¡ß0£¼e£¼1£¬¡à
¡Üe£¼1£¨5·Ö£©
£¨2£©¢Ùµ±e=
ʱµÃÍÖԲΪ
+
=1
ÉèH£¨x£¬y£©ÊÇÍÖÔ²ÉÏÒ»µã£¬
Ôò|HN|2=x2+£¨y-3£©2=£¨2b2-2y2£©+£¨y-3£©2=-£¨y+3£©2+2b2+18£¬£¨-b¡Üy¡Üb£©
£¨6·Ö£©
Éè0£¼b£¼3£¬Ôò-3£¼-b£¼0£¬µ±y=-bʱ£¬|HN|max2=b2+6b+9£¬£¬ÓÉÌâÒâµÃb2+6b+9=50
¡àb=-3¡À5
£¬Óë0£¼b£¼3ì¶Ü£¬£¨7·Ö£©
Éèb¡Ý3µÃ-b¡Ü-3£¬µ±y=-3ʱ£¬|HN|max2=2b2+18£¬£¬ÓÉ2b2+18=50µÃb2=16£¬£¨ºÏÌâÞ²£©
¡àÍÖÔ²·½³ÌÊÇ£º
+
=1£¨8·Ö£©
¢Ú£®Éèl£ºy=kx+mÓÉ
⇒(1+2k2)x2+4kmx+2m2-32=0
¶ø¡÷£¾0⇒m2£¼32k2+16£¨9·Ö£©
ÓÖA¡¢BÁ½µã¹ØÓÚ¹ýµãP(0£¬-
)¡¢QµÄÖ±Ï߶ԳÆ
¡àkPQ=-
£¬ÉèA£¨x1£¬y1£©£¬B£¨x2£¬y2£©£¬ÔòxQ=-
£¬yQ=
£¨10·Ö£©
¡à
=-
⇒m=
£¨11·Ö£©
¡à(
)2£¼32k2+16⇒0£¼k2£¼
£¨10·Ö£©
ÓÖk¡Ù0£¬¡à-
£¼k£¼0»ò0£¼k£¼
£¨11·Ö£©
¡àÐèÇóµÄkµÄÈ¡Öµ·¶Î§ÊÇ-
£¼k£¼0»ò0£¼k£¼
£¨12·Ö£©
| F1M |
| F2M |
ÓÉ
| F1M |
| F2M |
ÓÖMÔÚÍÖÔ²ÉÏ£¬¡ày2=b2-
| b2 |
| a2 |
¡àc2-x2=b2-
| b2 |
| a2 |
| a2b2 |
| c2 |
ÓÖ0¡Üx2¡Üa2¡à0£¼2-
| 1 |
| e2 |
| ||
| 2 |
¡ß0£¼e£¼1£¬¡à
| ||
| 2 |
£¨2£©¢Ùµ±e=
| ||
| 2 |
| x2 |
| 2b2 |
| y2 |
| b2 |
ÉèH£¨x£¬y£©ÊÇÍÖÔ²ÉÏÒ»µã£¬
Ôò|HN|2=x2+£¨y-3£©2=£¨2b2-2y2£©+£¨y-3£©2=-£¨y+3£©2+2b2+18£¬£¨-b¡Üy¡Üb£©
£¨6·Ö£©
Éè0£¼b£¼3£¬Ôò-3£¼-b£¼0£¬µ±y=-bʱ£¬|HN|max2=b2+6b+9£¬£¬ÓÉÌâÒâµÃb2+6b+9=50
¡àb=-3¡À5
| 2 |
Éèb¡Ý3µÃ-b¡Ü-3£¬µ±y=-3ʱ£¬|HN|max2=2b2+18£¬£¬ÓÉ2b2+18=50µÃb2=16£¬£¨ºÏÌâÞ²£©
¡àÍÖÔ²·½³ÌÊÇ£º
| x2 |
| 32 |
| y2 |
| 16 |
¢Ú£®Éèl£ºy=kx+mÓÉ
|
¶ø¡÷£¾0⇒m2£¼32k2+16£¨9·Ö£©
ÓÖA¡¢BÁ½µã¹ØÓÚ¹ýµãP(0£¬-
| ||
| 3 |
¡àkPQ=-
| 1 |
| k |
| 2km |
| 1+2k2 |
| m |
| 1+2k2 |
¡à
yQ+
| ||||
| xQ |
| 1 |
| k |
| 1+2k2 | ||
|
¡à(
| 1+2k2 | ||
|
| 47 |
| 2 |
ÓÖk¡Ù0£¬¡à-
| ||
| 2 |
| ||
| 2 |
¡àÐèÇóµÄkµÄÈ¡Öµ·¶Î§ÊÇ-
| ||
| 2 |
| ||
| 2 |

Á·Ï°²áϵÁдð°¸
Ïà¹ØÌâÄ¿
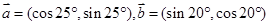 £¬Èô
£¬Èô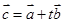 £¨
£¨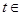
 £©£¬Ôò
£©£¬Ôò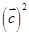 µÄ×îСֵΪ£¨ £©
µÄ×îСֵΪ£¨ £©