题目内容
17.某校高三年有375名学生,其中男生150人,女生225人.为调查该校高三年学生每天课外阅读的平均时间(单位:小时),采用分层抽样的方法从中随机抽取25人获得样本数据,该样本数据的频率分布直方图如图.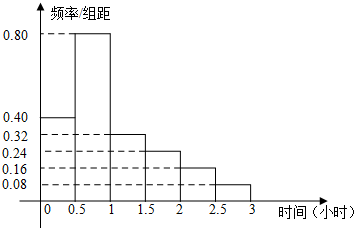
(Ⅰ)应抽取男生多少人?并根据样本数据,估计该校高三年学生每天课外阅读的平均时间;
(Ⅱ)在这25个样本中,从每天阅读平均时间不少于1.5小时的学生中任意抽取两人,求抽中的这两个人中恰有一个人的阅读平均时间不少于2小时的概率.
分析 (I)根据频率分布直方图可先求出应抽取男生人数,根据公式$\overline{{x}_{1}}{f}_{1}+\overline{{x}_{2}}{f}_{2}+…+\overline{{x}_{n}}{f}_{n}$可求平均阅读时间;
(Ⅱ)每天阅读平均时间不少于1.5小时的学生有6人,读平均时间不少于2小时有3人,列举出基本事件的个数,可求解概率.
解答 解:(I)应抽取男生$150×\frac{25}{375}=10$人,…(2分)
该校高三年学生每天课外阅读的平均时间为0.5×(0.40×0.25+0.80×0.75+0.32×1.25+0.24×1.75+0.16×2.25+0.08×2.75)=1.05,…(5分)
(Ⅱ)从每天阅读平均时间不少于1.5小时的学生有6人,…(6分)
其中读平均时间不少于2小时有3人,…(7分)
令这三人分别为A,B,C.另外三人为a,b,c,
设抽中的这两个人中恰有一个人的阅读平均时间不少于2小时为事件E,…(8分)
从中抽中的这两个人所有情况为(A,B),(A,C),(A,a),(A,b),(A,c),(B,C),(B,a),(B,b),(B,c),(C,a),(C,b),(C,c),(a,b),(a,c),(b,c)共15种,…(10分)
这两个人中恰有一个人的阅读平均时间不少于2小时的情况为(A,a),(A,b),(A,c),(B,a),(B,b),(B,c),(C,a),(C,b),(C,c)共9种…(11分)
∴抽中的这两个人中恰有一个人的阅读平均时间不少于2小时的概率为$P(E)=\frac{9}{15}=\frac{3}{5}$.…(12分)
点评 本题考查概率与统计,涉及频率分布直方图,属基础题.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目
8.函数g(x)=x3+($\frac{m}{2}$+2)x2-2x在(2,3)上总存在极值,则实数m的取值范围为( )
| A. | (-$\frac{58}{9}$,-6) | B. | (-$\frac{37}{3}$,-9) | C. | (-$\frac{37}{3}$,9) | D. | (-$\frac{37}{3}$,-6) |
2.在△ABC中,若(a+b+c)(c+b-a)=bc,则A=( )
| A. | A=150° | B. | A=120° | C. | A=60° | D. | A=30° |
6.如图给出的是计算1+3+5+…+99的一个程序框图,其中判断内应填入的条件是( )


| A. | i<99 | B. | i>99 | C. | i<100 | D. | i>100 |