题目内容
1.已知矩阵M=$(\begin{array}{l}{a}&{1}\\{b}&{1}\end{array})$的一个特征值l所对应的特征向量为$(\begin{array}{l}{1}\\{0}\end{array})$.(Ⅰ)求矩阵M的逆矩阵;
(Ⅱ)求曲线C:x2+2xy+2y2=1在矩阵M对应变换作用下得到的新的曲线方程.
分析 (Ⅰ)通过$[\begin{array}{l}{a}&{1}\\{b}&{1}\end{array}]$$[\begin{array}{l}{1}\\{0}\end{array}]$=1•$[\begin{array}{l}{1}\\{0}\end{array}]$可得a=1,b-0,进而可得结论;
(Ⅱ)通过设曲线C上任意一点(x,y)在矩阵M对应变换作用下得到(x′,y′),利用$[\begin{array}{l}{x′}\\{y′}\end{array}]$=$[\begin{array}{l}{1}&{1}\\{0}&{1}\end{array}]$$[\begin{array}{l}{x}\\{y}\end{array}]$,用x′、y′表示出x、y,并代入曲线C方程即得结论.
解答 解:(Ⅰ)依题意,$[\begin{array}{l}{a}&{1}\\{b}&{1}\end{array}]$$[\begin{array}{l}{1}\\{0}\end{array}]$=1•$[\begin{array}{l}{1}\\{0}\end{array}]$,
∴$[\begin{array}{l}{a}\\{b}\end{array}]$=$[\begin{array}{l}{1}\\{0}\end{array}]$,解得a=1,b-0,
∴M=$[\begin{array}{l}{1}&{1}\\{0}&{1}\end{array}]$,
∵detM=1≠0,所以M-1=$[\begin{array}{l}{1}&{-1}\\{0}&{1}\end{array}]$;
(Ⅱ)曲线C:x2+2xy+2y2=1上任意一点(x,y)
在矩阵M对应变换作用下得到(x′,y′),
则$[\begin{array}{l}{x′}\\{y′}\end{array}]$=$[\begin{array}{l}{1}&{1}\\{0}&{1}\end{array}]$$[\begin{array}{l}{x}\\{y}\end{array}]$,∴$\left\{\begin{array}{l}{x′=x+y}\\{y′=y}\end{array}\right.$,即$\left\{\begin{array}{l}{x=x′-y′}\\{y=y′}\end{array}\right.$,
代入方程x2+2xy+2y2=1,得(x′)2+(y′)2=1,
∴曲线C在矩阵M对应变换作用下得到的新的曲线方程为:x2+y2=1.
点评 本题考查矩阵与变换,注意解题方法的积累,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
| A. | 0 | B. | 锐角 | C. | $\frac{π}{2}$ | D. | 钝角 |
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 4 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
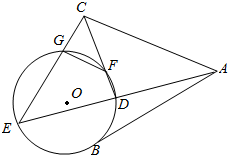 如图,AB是圆O的一条切线,切点为B,ADE,CFD,CGE都是圆O的割线,已知AC=AB.
如图,AB是圆O的一条切线,切点为B,ADE,CFD,CGE都是圆O的割线,已知AC=AB.