题目内容
已知函数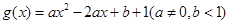 在区间
在区间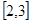 上有最大值4,最小值1,
上有最大值4,最小值1,
(Ⅰ)求 的值。
的值。
(Ⅱ)设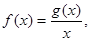 不等式
不等式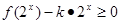 在区间
在区间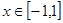 上恒成立,求实数k的取值范围?
上恒成立,求实数k的取值范围?
(Ⅰ)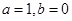 ;(Ⅱ)
;(Ⅱ)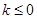 .
.
解析试题分析:(Ⅰ)函数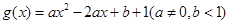 在区间
在区间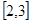 上有最大值4,最小值1,求
上有最大值4,最小值1,求 的值,由二次函数
的值,由二次函数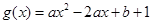 的对称轴为
的对称轴为 ,对称轴在区间
,对称轴在区间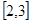 的左侧,在区间
的左侧,在区间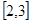 上是单调函数,由于不知
上是单调函数,由于不知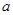 的值,需讨论,由已知可知
的值,需讨论,由已知可知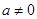 ,分
,分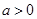 ,
,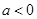 两种情况,结合单调性,即
两种情况,结合单调性,即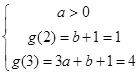 ,或
,或 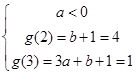 ,解出
,解出 的值,注意
的值,注意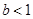 这个条件,把不符合的舍去;
这个条件,把不符合的舍去;
(Ⅱ)设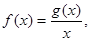 不等式
不等式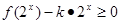 在区间
在区间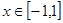 上恒成立,求实数k的取值范围,首先求出函数
上恒成立,求实数k的取值范围,首先求出函数 的解析式,此题属于恒成立问题,解这一类题,常常采用含有参数
的解析式,此题属于恒成立问题,解这一类题,常常采用含有参数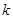 的放到不等式的一边,不含参数
的放到不等式的一边,不含参数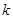 (即含
(即含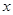 )的放到不等式的另一边,转化为函数的最值问题,故不等式可化为
)的放到不等式的另一边,转化为函数的最值问题,故不等式可化为 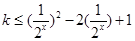 ,在
,在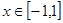 时,
时,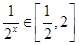 ,则
,则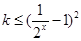 ,根据
,根据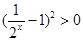 ,求得实数
,求得实数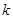 的取值范围.
的取值范围.
试题解析:(Ⅰ)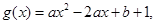 对称轴
对称轴 ,在区间
,在区间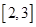
①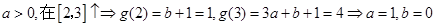
②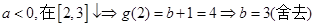
综上,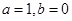 .(6分)
.(6分)
(Ⅱ)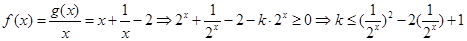
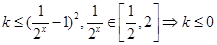 (12分)
(12分)
考点:二次函数在闭区间上的最值,求函数的解析式解,指数型复合函数的性质及应用.

练习册系列答案
相关题目
某市一家庭今年一月份、二月份、和三月份煤气用量和支付费用如下表所示:
| 月份 | 用气量(立方米) | 煤气费(元) |
| 1 | 4 | 4.00 |
| 2 | 25 | 14.00 |
| 3 | 35 | 19.00 |
若每月用气量不超过最低额度
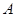
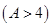 立方米时,只付基本费3元+每户每月定额保险费
立方米时,只付基本费3元+每户每月定额保险费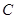
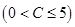 元;若用气量超过
元;若用气量超过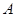 立方米时,超过部分每立方米付
立方米时,超过部分每立方米付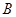 元.
元.⑴根据上面的表格求
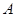 、
、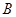 、
、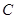 的值;
的值;⑵若用户第四月份用气30立方米,则应交煤气费多少元?
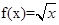 (0<x≤1),求x∈[-5,-4]时,函数f(x)的解析式.
(0<x≤1),求x∈[-5,-4]时,函数f(x)的解析式. ,则股价
,则股价 (元)和时间
(元)和时间 的关系在
的关系在 段可近似地用解析式
段可近似地用解析式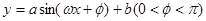 来描述,从
来描述,从 点走到今天的
点走到今天的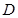 点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且
点,是震荡筑底阶段,而今天出现了明显的筑底结束的标志,且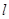 :
: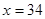 对称。老张预计这只股票未来的走势如图中虚线所示,这里
对称。老张预计这只股票未来的走势如图中虚线所示,这里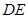 段与
段与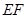 段是股价延续
段是股价延续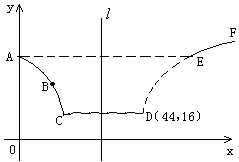
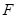 。现在老张决定取点
。现在老张决定取点
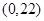 ,点
,点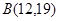 ,点
,点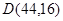 来确定解析式中的常数
来确定解析式中的常数 ,
,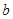 ,
,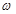 ,
,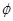 ,并且求得
,并且求得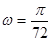 。
。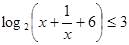 ;
;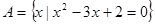 ,
,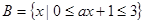 .若
.若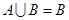 ,求实数
,求实数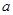 的取值组成的集合.
的取值组成的集合.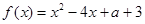 ,
,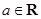 .
. 的图象与
的图象与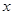 轴无交点,求
轴无交点,求 的取值范围;
的取值范围;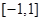 上存在零点,求
上存在零点,求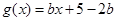 ,
,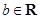 .当
.当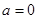 时,若对任意的
时,若对任意的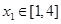 ,总存在
,总存在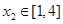 ,使得
,使得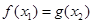 ,求
,求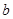 的取值范围.
的取值范围.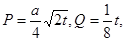 其中
其中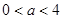 ,今该公司将5亿元投资这两个项目,其中对甲项目投资x(亿元),投资这两个项目所获得的总利润为y(亿元),
,今该公司将5亿元投资这两个项目,其中对甲项目投资x(亿元),投资这两个项目所获得的总利润为y(亿元),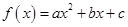 .
.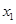 、
、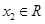 ,且
,且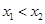 ,都有
,都有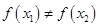 ,求证:关于
,求证:关于 的方程
的方程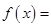
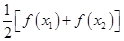 有两个不相等的实数根且必有一个根属于
有两个不相等的实数根且必有一个根属于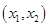 ;
;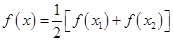 在
在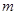 ,且
,且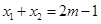 ,设函数
,设函数 的图象的对称轴方程为
的图象的对称轴方程为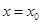 ,求证:
,求证: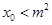 .
.