题目内容
(1)解不等式: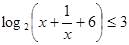 ;
;
(2)已知集合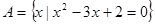 ,
,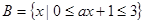 .若
.若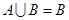 ,求实数
,求实数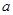 的取值组成的集合.
的取值组成的集合.
(1)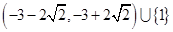 ;(2)
;(2)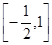 .
.
解析试题分析:(1)本题是一个对数不等式问题的求解问题,解不等式时,先由对数函数的单调性得到真数的取值范围,不要忘记了真数为正的要求,此时就可化为一般的分式不等式解之即可,分式不等式要去分母时,要注意符号的讨论;(2)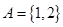 ,由
,由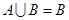 知
知 ,要具体化集合
,要具体化集合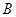 的过程中,要解一个含有参数的不等式,要对参数进行分类讨论,然后对各种情况下的结果利用
的过程中,要解一个含有参数的不等式,要对参数进行分类讨论,然后对各种情况下的结果利用 解决问题,较为简单的做法是,集合
解决问题,较为简单的做法是,集合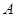 中的元素都在集合
中的元素都在集合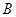 ,都满足不等式,代入即可解决问题.
,都满足不等式,代入即可解决问题.
试题解析:(1)由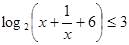 得,
得,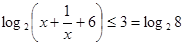
∴ .
.
由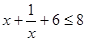 解得
解得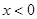 或
或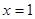
由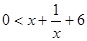 解得
解得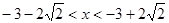 或
或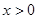
从而得原不等式的解集为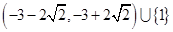 .
.
(2)法一:∵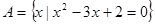
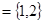 ,
,
又∵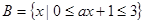
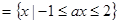 ,
,
∵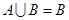 ,∴
,∴
①当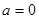 时,
时,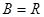 ,满足题意.
,满足题意.
②当 时,
时,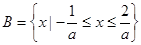 ,∵
,∵ ∴
∴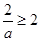 ,解得
,解得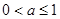 .
.
③当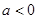 时,
时,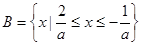 ,∵
,∵ ∴
∴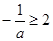 ,解得
,解得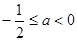 .
.
综上,实数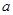 的取值组成的集合为
的取值组成的集合为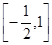 .
.
法二:∵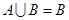 ,∴
,∴
又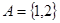 ,∴
,∴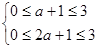 ∴
∴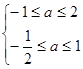 ,∴
,∴ .
.
∴实数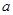 的取值组成的集合为
的取值组成的集合为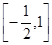 .
.
考点:对数函数的性质、解不等式、集合的包含关系.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
 为实数,函数
为实数,函数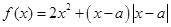 .
.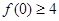 ,求
,求 的最小值.
的最小值.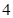 元,并且每件商品需向总店交
元,并且每件商品需向总店交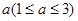 元的管理费,预计当每件商品的售价为
元的管理费,预计当每件商品的售价为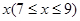 元时,一年的销售量为
元时,一年的销售量为 万件.
万件.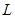 (万元)与每件商品的售价
(万元)与每件商品的售价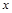 的函数关系式
的函数关系式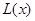 ;
;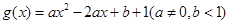 在区间
在区间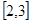 上有最大值4,最小值1,
上有最大值4,最小值1, 的值。
的值。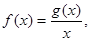 不等式
不等式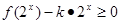 在区间
在区间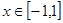 上恒成立,求实数k的取值范围?
上恒成立,求实数k的取值范围?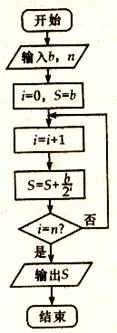
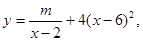 其中2<x<6,m为常数,已知销售价格为4元/件时,每月可售出21千件。(1)求m的值; (2)假设该淘宝店员工工资、办公等每月所有开销折合为每件2元(只考虑销售出的件数),试确定销售价格x的值,使该店每月销售饰品所获得的利润最大.(结果保留一位小数)
其中2<x<6,m为常数,已知销售价格为4元/件时,每月可售出21千件。(1)求m的值; (2)假设该淘宝店员工工资、办公等每月所有开销折合为每件2元(只考虑销售出的件数),试确定销售价格x的值,使该店每月销售饰品所获得的利润最大.(结果保留一位小数)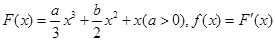 ,若
,若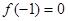 且对任意实数
且对任意实数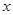 均有
均有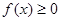 成立.
成立.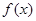 表达式;
表达式;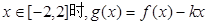 是单调函数,求实数
是单调函数,求实数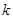 的取值范围.
的取值范围.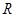 上的函数
上的函数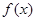 对任意
对任意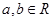 都有
都有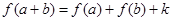 (
(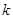 为常数).
为常数).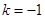 ,
,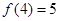 ,若不等式
,若不等式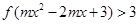 对任意
对任意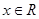 恒成立,求实数
恒成立,求实数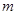 的取值范围.
的取值范围.