题目内容
已知函数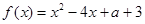 ,
,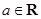 .
.
(Ⅰ)若函数 的图象与
的图象与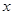 轴无交点,求
轴无交点,求 的取值范围;
的取值范围;
(Ⅱ)若函数 在
在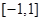 上存在零点,求
上存在零点,求 的取值范围;
的取值范围;
(Ⅲ)设函数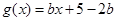 ,
,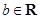 .当
.当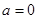 时,若对任意的
时,若对任意的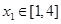 ,总存在
,总存在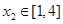 ,使得
,使得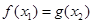 ,求
,求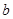 的取值范围.
的取值范围.
(Ⅰ) ;(Ⅱ)
;(Ⅱ)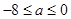 ;(Ⅲ)
;(Ⅲ)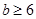 或
或 .
.
解析试题分析:(Ⅰ)函数 的图像与
的图像与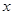 轴无交点,那么函数对应的方程的判别式
轴无交点,那么函数对应的方程的判别式 ,解不等式即可;(Ⅱ)先判断函数
,解不等式即可;(Ⅱ)先判断函数 在闭区间
在闭区间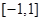 的单调性,然后根据零点存在性定理,可知
的单调性,然后根据零点存在性定理,可知 ,解方程组求得同时满足两个表达式的
,解方程组求得同时满足两个表达式的 的取值范围;(Ⅲ)若对任意的
的取值范围;(Ⅲ)若对任意的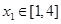 ,总存在
,总存在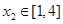 ,使
,使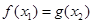 ,只需函数
,只需函数 的值域为函数
的值域为函数 值域的子集即可.先求出函数
值域的子集即可.先求出函数 在区间
在区间 上的值域是
上的值域是 ,然后判断函数
,然后判断函数 的值域.分
的值域.分 ,
, ,
, 三种情况进行分类讨论,当
三种情况进行分类讨论,当 时,函数
时,函数 是一次函数,最值在两个区间端点处取得,所以假设其值域是
是一次函数,最值在两个区间端点处取得,所以假设其值域是 ,那么就有
,那么就有 成立,解相应的不等式组即可.
成立,解相应的不等式组即可.
试题解析:(Ⅰ)若函数 的图象与
的图象与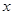 轴无交点,则方程
轴无交点,则方程 的判别式
的判别式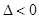 ,
,
即 ,解得
,解得 . 3分
. 3分
(Ⅱ)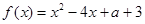 的对称轴是
的对称轴是 ,所以
,所以 在
在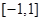 上是减函数,
上是减函数, 在
在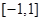 上存在零点,则必有:
上存在零点,则必有: ,即
,即 ,
,
解得: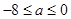 ,故实数
,故实数 的取值范围为
的取值范围为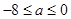 ; 8分
; 8分
(Ⅲ)若对任意的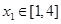 ,总存在
,总存在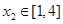 ,使
,使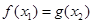 ,只需函数
,只需函数 的值域为函数
的值域为函数 值域的子集.当
值域的子集.当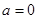 时,
时,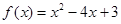 的对称轴是
的对称轴是 ,所以
,所以 的值域为
的值域为 , 下面求
, 下面求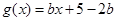 ,
,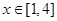 的值域,
的值域,
①当 时,
时, ,不合题意,舍;
,不合题意,舍;
②当 时,
时,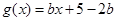 的值域为
的值域为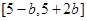 ,只需要:
,只需要: ,解得
,解得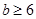 ;
;
③当 时,
时,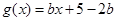 的值域为
的值域为 ,只需要:
,只需要: ,解得
,解得 ;
;
综上:实数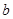 的取值范围
的取值范围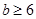 或
或 . 14分
. 14分
考点:1.方程根的个数与判别式的关系;2.零点存在性定理;3.二次函数在闭区间上的值域;4.一次函数的单调性;5.二次函数的图像与性质

练习册系列答案
相关题目
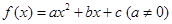 满足
满足 ,对任意
,对任意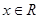 都有
都有 ,且
,且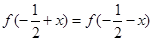 .
. 的解析式;
的解析式;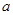 ,使函数
,使函数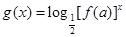 在
在 上为减函数?若存在,求出实数
上为减函数?若存在,求出实数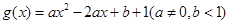 在区间
在区间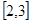 上有最大值4,最小值1,
上有最大值4,最小值1, 的值。
的值。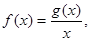 不等式
不等式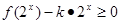 在区间
在区间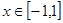 上恒成立,求实数k的取值范围?
上恒成立,求实数k的取值范围? ,
, ,其中实数
,其中实数 .
. ,求函数
,求函数 的单调区间;
的单调区间; 与
与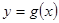 的图象只有一个公共点且
的图象只有一个公共点且 存在最小值时,记
存在最小值时,记 ,求
,求 内均为增函数,求实数
内均为增函数,求实数 的取值范围.
的取值范围.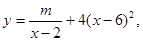 其中2<x<6,m为常数,已知销售价格为4元/件时,每月可售出21千件。(1)求m的值; (2)假设该淘宝店员工工资、办公等每月所有开销折合为每件2元(只考虑销售出的件数),试确定销售价格x的值,使该店每月销售饰品所获得的利润最大.(结果保留一位小数)
其中2<x<6,m为常数,已知销售价格为4元/件时,每月可售出21千件。(1)求m的值; (2)假设该淘宝店员工工资、办公等每月所有开销折合为每件2元(只考虑销售出的件数),试确定销售价格x的值,使该店每月销售饰品所获得的利润最大.(结果保留一位小数) ,
, ,其中实数
,其中实数 .
. ,求函数
,求函数 的单调区间;
的单调区间; 与
与 的图象只有一个公共点且
的图象只有一个公共点且 存在最小值时,记
存在最小值时,记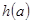 ,求
,求 内均为增函数,求实数
内均为增函数,求实数 的取值范围.
的取值范围. (
( 为常数,
为常数, 为自然对数的底)
为自然对数的底)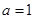 时,求
时,求 的单调区间;
的单调区间; 上无零点,求
上无零点,求 ,在
,在 上存在两个不同的
上存在两个不同的 使得
使得 成立,求
成立,求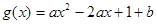 (
(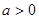 )在区间
)在区间 上有最大值
上有最大值 和最小值
和最小值 .设
.设 ,
,  、
、 的值;
的值; 在
在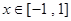 上有解,求实数
上有解,求实数 的取值范围.
的取值范围.