题目内容
已知函数f(x)是定义在R上的奇函数,且f(x)的图象关于直线x=1对称.
(1)求证:f(x)是周期为4的周期函数;
(2)若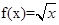 (0<x≤1),求x∈[-5,-4]时,函数f(x)的解析式.
(0<x≤1),求x∈[-5,-4]时,函数f(x)的解析式.
(1)见解析;(2)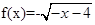 .
.
解析试题分析:(1)只需证明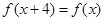 .由函数f(x)的图象关于直线
.由函数f(x)的图象关于直线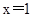 对称,可得
对称,可得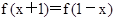 ,
,
即有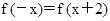 .根据函数
.根据函数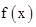 是定义在R上的奇函数,故有
是定义在R上的奇函数,故有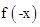 =-
=-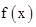 .
.
从而由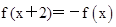 ,得到
,得到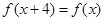 ,即f(x)是周期为4的周期函数.
,即f(x)是周期为4的周期函数.
(2)首先由函数f(x)是定义在R上的奇函数,得到f(0)=0.
根据x∈[-1,0)时,-x∈(0,1],f(x)=-f(-x)=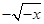 .
.
利用函数的周期性得到,x∈[-5,-4]时,函数f(x)的解析式.
试题解析:(1)证明:由函数f(x)的图象关于直线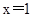 对称,有
对称,有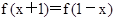 ,
,
即有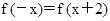 2分
2分
又函数f(x)是定义在R上的奇函数,故有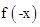 =-
=-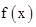 .
.
故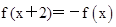 ,从而
,从而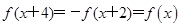 ,即
,即 是周期为4的周期函数. 6分
是周期为4的周期函数. 6分
(2)由函数f(x)是定义在R上的奇函数,可知f(0)=0.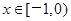 时,
时,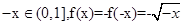 .
.
故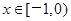 时,
时,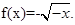 9分
9分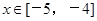 时,
时,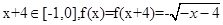 .
.
从而,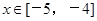 时,函数f(x)的解析式为
时,函数f(x)的解析式为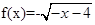 . 12分
. 12分
考点:函数的奇偶性、周期性

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 毫米,滴管内液体忽略不计.
毫米,滴管内液体忽略不计.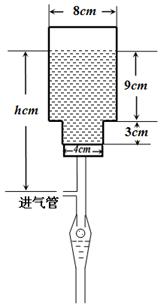
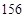 分钟滴完,问每分钟应滴下多少滴?
分钟滴完,问每分钟应滴下多少滴?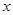 (单位:分钟),瓶内液面与进气管的距离为
(单位:分钟),瓶内液面与进气管的距离为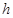 (单位:厘米),已知当
(单位:厘米),已知当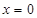 时,
时,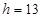 .试将
.试将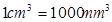 )
) 的定义域为
的定义域为 ,且同时满足以下三个条件:①
,且同时满足以下三个条件:①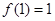 ;②对任意的
;②对任意的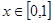 ,都有
,都有 ;③当
;③当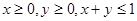 时总有
时总有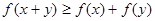 .
.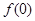 的值;
的值;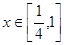 时,恒有
时,恒有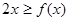 .
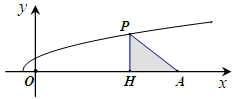
.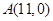 ,函数
,函数 的图象上的动点
的图象上的动点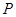 在
在 轴上的射影为
轴上的射影为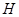 ,且点
,且点 的左侧.设
的左侧.设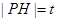 ,
,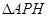 的面积为
的面积为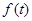 .
.
 的取值范围;
的取值范围;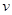 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度 (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过40辆/千米时,车流速度为80千米/小时.研究表明:当
(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过40辆/千米时,车流速度为80千米/小时.研究表明:当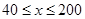 时,车流速度
时,车流速度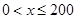 时,求函数
时,求函数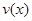 的表达式;
的表达式;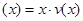 ,
,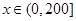 可以达到最大,并求出最大值.
可以达到最大,并求出最大值.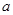 为实数,函数
为实数,函数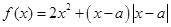 .
.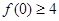 ,求
,求 的最小值.
的最小值.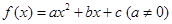 满足
满足 ,对任意
,对任意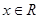 都有
都有 ,且
,且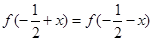 .
. 的解析式;
的解析式;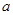 ,使函数
,使函数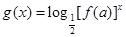 在
在 上为减函数?若存在,求出实数
上为减函数?若存在,求出实数 }的前n项和为为
}的前n项和为为 ,且
,且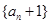 是等比数列;
是等比数列;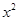 +ax-1的零点,若关于x的不等式f(x)≥
+ax-1的零点,若关于x的不等式f(x)≥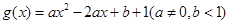 在区间
在区间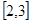 上有最大值4,最小值1,
上有最大值4,最小值1, 的值。
的值。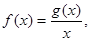 不等式
不等式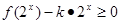 在区间
在区间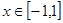 上恒成立,求实数k的取值范围?
上恒成立,求实数k的取值范围?