题目内容
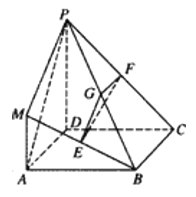
【题目】如图①,在△ABC中,已知AB=15,BC=14,CA=13.将△ABC沿BC边上的高AD折成一个如图②所示的四面体A﹣BCD,使得图②中的BC=11. 
(1)求二面角B﹣AD﹣C的平面角的余弦值;
(2)在四面体A﹣BCD的棱AD上是否存在点P,使得 ![]() =0?若存在,请指出点P的位置;若不存在,请给出证明.
=0?若存在,请指出点P的位置;若不存在,请给出证明.
【答案】
(1)解:由已知AD⊥BD,AD⊥CD,
故二面角B﹣AD﹣C的平面角为∠BDC,
在图①,设BD=x,AD=h,则CD=14﹣x,
在△ABD与△ACD中,分别用勾股定理得x2+h2=152,(14﹣x)2+h2=132,
得x=9,h=12,从而AD=12,BD=9,CD=5,
在图②的△BCD中,由余弦定理得BC2=BD2+CD2﹣2BDCDcos∠BDC,
即112=92+52﹣2×9×5cos∠BDC,则cos∠BDC=﹣ ![]() ,
,
即二面角B﹣AD﹣C的平面角的余弦值是﹣ ![]()
(2)解:假设在四面体A﹣BCD的棱AD上存在点P,使得 ![]() ,
,
则0= ![]() =(
=( ![]() +
+ ![]() )(
)( ![]() +
+ ![]() )=
)= ![]() 2+
2+ ![]()
![]() +
+ ![]()
![]() +
+ ![]()
![]() =
= ![]() 2+0+0+9×5×(﹣
2+0+0+9×5×(﹣ ![]() )=
)= ![]() 2﹣
2﹣ ![]() ,
,
则| ![]() |=
|= ![]() <12,符号题意,
<12,符号题意,
即在棱AD上存在点P,使得 ![]() ,此时|
,此时| ![]() |=
|= ![]()
【解析】(1)根据图象折之前和折之后的边长关系,合二面角的定义进行求解.(2)假设在四面体A﹣BCD的棱AD上存在点P,使得 ![]() 根据向量数量积的定义结合向量的运算法则进行化简求解.
根据向量数量积的定义结合向量的运算法则进行化简求解.

练习册系列答案
相关题目