题目内容
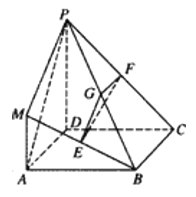
【题目】在如图所示的几何体中,四边形![]() 是正方形,
是正方形, ![]() 平面
平面![]() ,
, ![]() 分别为
分别为![]() 的中点,且
的中点,且![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)求三棱锥![]() 与四棱锥
与四棱锥![]() 的体积之比.
的体积之比.
【答案】(1)证明过程详见解析(2)证明过程详见解析;(3)1:4
【解析】
(1)由三角形中位线定理可得![]() ,由正方形的性质可得
,由正方形的性质可得![]() ,
,![]() ,由线面平行的判定定理可得
,由线面平行的判定定理可得![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,从而可得结果;(2)由线面垂直的性质证明
,从而可得结果;(2)由线面垂直的性质证明![]() ,正方形的性质可得
,正方形的性质可得![]() ,结合
,结合![]() ,可得
,可得![]() 平面
平面![]() ,从而可得平面
,从而可得平面![]() 平面
平面![]() ;(3)求出
;(3)求出![]() ,则
,则![]() ,得到
,得到![]() 平面
平面![]() ,求出
,求出![]() ,即
,即![]() 即为点
即为点![]() 到平面
到平面![]() 的距离,根据三棱锥的体积公式求出体积得到比值.
的距离,根据三棱锥的体积公式求出体积得到比值.
(1)∵![]() 分别为
分别为![]() 的中点,
的中点,
∴![]() ,
,
又∵四边形![]() 是正方形,
是正方形,
∴![]() ,∴
,∴![]() ,
,
∵![]() 在平面
在平面![]() 外,
外, ![]() 在平面
在平面![]() 内,
内,
∴![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
又∵![]() 都在平面
都在平面![]() 内且相交,
内且相交,
∴平面![]() 平面
平面![]() .
.
(2)证明:由已知![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,∴
,∴![]() .
.
∵四边形![]() 为正方形,∴
为正方形,∴![]() ,
,
又![]() ,∴
,∴![]() 平面
平面![]() ,
,
在![]() 中,∵
中,∵![]() 分别为
分别为![]() 的中点,
的中点,
∴![]() ,∴
,∴![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
(3)解:∵![]() 平面
平面![]() ,四边形
,四边形![]() 为正方形,
为正方形,![]() ,则
,则![]() .
.
∵![]() 平面
平面![]() ,且
,且![]() ,
,
∴![]() 即为点
即为点![]() 到平面
到平面![]() 的距离,
的距离,
∴![]() =
=![]()

练习册系列答案
相关题目
【题目】两个随机变量x,y的取值表为
x | 0 | 1 | 3 | 4 |
y | 2.2 | 4.3 | 4.8 | 6.7 |
若x,y具有线性相关关系,且 ![]() =
= ![]() x+2.6,则下列四个结论错误的是( )
x+2.6,则下列四个结论错误的是( )
A.x与y是正相关
B.当x=6时,y的估计值为8.3
C.x每增加一个单位,y增加0.95个单位
D.样本点(3,4.8)的残差为0.56