Question

【题目】定义在R上的奇函数f(x)满足f(x＋2)＝－f(x)，当0≤x≤1时，f(x)＝x，

(1)试画出f(x)，x∈[－3,5]的图象；

(2)求f(37.5)；

(3)常数a∈(0,1)，y＝a与f(x)，x∈[－3,5]的图象相交，求所有交点横坐标之和．

Answer 1

【答案】（1）见解析； （2） ； （3）4.

【解析】

(1)由题得函数的图像关于原点对称，关于直线x=1对称，依次性质作出函数的图像.(2)由图可知f(x＋4)＝f(x)，所以函数的周期是4，再利用周期性求值.(3) 由图可知，当a∈(0,1)时，y＝a与f(x)，x∈[－3,5]有4个交点，设为x1，x2，x3，x4(x1<x2<x3<x4)．由图可知＝－1，＝3.即得所有交点横坐标之和．

(1)∵f(x)为奇函数，

∴f(x＋2)＝f(－x)，

∴f(x)关于直线x＝1对称．

由f(x)在[0,1]上的图象反复关于(0,0)，x＝1对称，可得f(x)，x∈[－3,5]的图象如图．

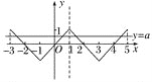
(2)由图可知f(x＋4)＝f(x)，

∴f(37.5)＝f(4×9＋1.5)＝f(1.5)＝f(0.5)＝.

(3)由图可知，当a∈(0,1)时，y＝a与f(x)，x∈[－3,5]有4个交点，设为x1，x2，x3，x4(x1<x2<x3<x4)．

由图可知＝－1，＝3.

∴x1＋x2＋x3＋x4＝－2＋6＝4.