题目内容
【题目】已知椭圆 ![]() +
+ ![]() =1(a>b>0)的左右焦点F1 , F2其离心率为e=
=1(a>b>0)的左右焦点F1 , F2其离心率为e= ![]() ,点P为椭圆上的一个动点,△PF1F2内切圆面积的最大值为
,点P为椭圆上的一个动点,△PF1F2内切圆面积的最大值为 ![]() .
.
(1)求a,b的值
(2)若A、B、C、D是椭圆上不重合的四个点,且满足 ![]() ,
, ![]() =0,求|
=0,求| ![]() |+|
|+| ![]() |的取值范围.
|的取值范围.
【答案】
(1)解:设△PF1F2内切圆半径为r,
由△PF1F2的面积为S= ![]() r(PF1+PF2+F1F2)=
r(PF1+PF2+F1F2)= ![]() r(2a+2c),
r(2a+2c),
S最大,则r最大,
当P为椭圆上下顶点时,△PF1F2的面积最大,其内切圆面积取得最大值,
∵ ![]() ,∴
,∴ ![]() .
.
![]() =
= ![]() =bc=
=bc= ![]() r=
r= ![]() ,化为
,化为 ![]() ,
,
又 ![]() ,a2=b2+c2,联立解得a=4,c=2,b=2
,a2=b2+c2,联立解得a=4,c=2,b=2 ![]()
(2)解:∵满足 ![]() =0,
=0,
∴直线AC,BD垂直相交于点F1,
由(1)椭圆方程 ![]() ,F1(﹣2,0).
,F1(﹣2,0).
①直线AC,BD有一条斜率不存在时,| ![]() |+|
|+| ![]() |=6+8=14.
|=6+8=14.
②当AC斜率存在且不为0时,设方程y=k(x+2),A(x1,y1),C(x2,y2),
联立 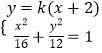 ,化为(3+4k2)x2+16k2x+16k2﹣48=0.
,化为(3+4k2)x2+16k2x+16k2﹣48=0.
∴x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ,
,
把﹣ ![]() 代入上述可得:可得|
代入上述可得:可得| ![]() |=
|= ![]() ,
,
∴| ![]() |+|
|+| ![]() |=
|= ![]() ,
,
设t=k2+1(k≠0),t>1.
∴| ![]() |+|
|+| ![]() |=
|= ![]() ,∵t>1,∴
,∵t>1,∴ ![]() ,
,
∴| ![]() |+|
|+| ![]() |∈
|∈ ![]() .
.
综上可得:| ![]() |+|
|+| ![]() |的取值范围是
|的取值范围是 ![]()
【解析】(1)当P为椭圆上下顶点时,△PF1F2内切圆面积取得最大值,设△PF1F2内切圆半径为r,利用 ![]() =
= ![]() =bc=
=bc= ![]() r,化为
r,化为 ![]() ,又
,又 ![]() ,a2=b2+c2 , 联立解得a,c,b即可得出.(2)由满足
,a2=b2+c2 , 联立解得a,c,b即可得出.(2)由满足 ![]() ,
, ![]() =0,可得直线AC,BD垂直相交于点F1 , 由(1)椭圆方程
=0,可得直线AC,BD垂直相交于点F1 , 由(1)椭圆方程 ![]() ,F1(﹣2,0).①直线AC,BD有一条斜率不存在时,|
,F1(﹣2,0).①直线AC,BD有一条斜率不存在时,| ![]() |+|
|+| ![]() |=14.②当AC斜率存在且不为0时,设方程y=k(x+2),A(x1 , y1),C(x2 , y2),与椭圆方程联立化为(3+4k2)x2+16k2x+16k2﹣48=0.利用根与系数的关系可得:
|=14.②当AC斜率存在且不为0时,设方程y=k(x+2),A(x1 , y1),C(x2 , y2),与椭圆方程联立化为(3+4k2)x2+16k2x+16k2﹣48=0.利用根与系数的关系可得: ![]() =
= ![]() =
= ![]() ,把﹣
,把﹣ ![]() 代入上述可得:可得|
代入上述可得:可得| ![]() |=
|= ![]() ,可得|
,可得| ![]() |+|
|+| ![]() |=
|= ![]() ,设t=k2+1(k≠0),t>1.即可得出.
,设t=k2+1(k≠0),t>1.即可得出.