题目内容
1.已知函数y=1+sinx(1)求函数y的定义域,值域;
(2)求函数y在其定义域上的单调递增区间;
(3)用“五点法”做出函数y在x∈[0,2π]上的简图.
分析 (1)根据正弦函数的定义域、值域,求得函数y=1+sinx的定义域,值域.
(2)根据正弦函数的单调性求得函数y=1+sinx的增区间.
(3)用五点法作函数y=1+sinx在一个周期上的简图.
解答 解:(1)对于函数y=1+sinx,根据t=sinx的定义域为R,值域为[-1,1],可得它的定义域为R,值域为[0,2].
(2)函数y=1+sinx的增区间即t=sinx的增区间,为[2kπ-$\frac{π}{2}$,2kπ+$\frac{π}{2}$].
(3)列表:
| x | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| y | 1 | 2 | 1 | 0 | 1 |
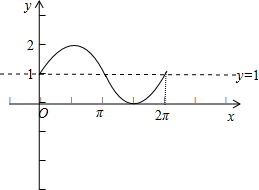
点评 本题主要考查正弦函数的定义域、值域和单调性,用五点法作函数y=Asin(ωx+φ)在一个周期上的简图,属于基础题.

练习册系列答案
相关题目
12.在复平面上,复数z=a+bi(a,b∈R)与复数i(i-2)关于实轴对称,则a+b的值为( )
| A. | 1 | B. | -3 | C. | 3 | D. | 2 |
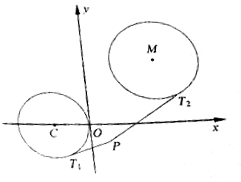 设圆C:(x+4)2+y2=16,动圆M:x2+y2-2ax-2(8-a)y+4a+22=0,平面内是还有存在定点P,过点P作圆C的一条切线,切点为T1,过点P作圆M的一条切线,切点为T2,使无穷多个圆M,满足$\frac{P{T}_{1}}{P{T}_{2}}$=$\frac{1}{2}$?如果存在,求出所有这样的点P;如果不存在,请说明理由.
设圆C:(x+4)2+y2=16,动圆M:x2+y2-2ax-2(8-a)y+4a+22=0,平面内是还有存在定点P,过点P作圆C的一条切线,切点为T1,过点P作圆M的一条切线,切点为T2,使无穷多个圆M,满足$\frac{P{T}_{1}}{P{T}_{2}}$=$\frac{1}{2}$?如果存在,求出所有这样的点P;如果不存在,请说明理由.