题目内容
10.“a>3”是“函数f(x)=ax+3在(-1,2)上存在零点”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 根据a>3判断出:f(-1)=-a+3<0、f(2)=2a+3>0,得到充分性成立;再由函数的零点存在性定理列出不等式求出a的范围,可得到必要性不成立.
解答 解:①充分性:当a>3时,f(-1)=-a+3<0、f(2)=2a+3>0,
所以函数f(x)=ax+3在(-1,2)上存在零点”,成立;
②因为函数f(x)=ax+3在(-1,2)上存在零点,
所以f(-1)f(2)<0,则(-a+3)(2a+3)<0,
即(a-3)(2a+3)>0,解得a>3或a<$-\frac{3}{2}$,不成立,
综上可得,“a>3”是“函数f(x)=ax+3在(-1,2)上存在零点”是充分不必要条件,
故选:A.
点评 本题考查了充要条件的判断,以及函数的零点存在性定理的应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.复数z=$\frac{3+i}{1-i}$(i为虚数单位)在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
19.“a>b>0,c>d>0”是“ac>bd>0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
20.在△ABC中,角A,B,C所对的边分别为a,b,c,已知a=2$\sqrt{3}$,c=2$\sqrt{2}$,1+$\frac{tanA}{tanB}$=$\frac{2c}{b}$.则∠C=( )
| A. | 30° | B. | 135° | C. | 45°或135° | D. | 45° |
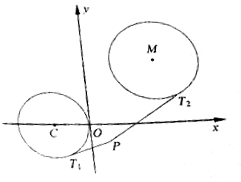 设圆C:(x+4)2+y2=16,动圆M:x2+y2-2ax-2(8-a)y+4a+22=0,平面内是还有存在定点P,过点P作圆C的一条切线,切点为T1,过点P作圆M的一条切线,切点为T2,使无穷多个圆M,满足$\frac{P{T}_{1}}{P{T}_{2}}$=$\frac{1}{2}$?如果存在,求出所有这样的点P;如果不存在,请说明理由.
设圆C:(x+4)2+y2=16,动圆M:x2+y2-2ax-2(8-a)y+4a+22=0,平面内是还有存在定点P,过点P作圆C的一条切线,切点为T1,过点P作圆M的一条切线,切点为T2,使无穷多个圆M,满足$\frac{P{T}_{1}}{P{T}_{2}}$=$\frac{1}{2}$?如果存在,求出所有这样的点P;如果不存在,请说明理由.