题目内容
16.已知函数f(x)=$\left\{\begin{array}{l}\frac{1}{x+2},-1≤x≤0\\{x}^{2}-2x,0<x≤1\end{array}\right.$,若f(2m-1)<$\frac{1}{2}$,则m的取值范围是( )| A. | m>$\frac{1}{2}$ | B. | m$<\frac{1}{2}$ | C. | 0$≤m<\frac{1}{2}$ | D. | $\frac{1}{2}<m≤1$ |
分析 由已知中函数f(x)=$\left\{\begin{array}{l}\frac{1}{x+2},-1≤x≤0\\{x}^{2}-2x,0<x≤1\end{array}\right.$,分2m-1∈[-1,0]和2m-1∈(0,1]两种情况,分别求出满足条件的m值,可得答案.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}\frac{1}{x+2},-1≤x≤0\\{x}^{2}-2x,0<x≤1\end{array}\right.$,
当2m-1∈[-1,0],即m∈[0,$\frac{1}{2}$]时,
f(2m-1)<$\frac{1}{2}$可化为:$\frac{1}{2m-1+2}<\frac{1}{2}$,
解得:m<-$\frac{1}{2}$,或m>$\frac{1}{2}$,
此时不存在满足条件的m值;
当2m-1∈(0,1],即m∈[$\frac{1}{2}$,1]时,
f(2m-1)<$\frac{1}{2}$可化为:$(2m-1)^{2}-2(2m-1)<\frac{1}{2}$,
解得:m∈[$1-\frac{\sqrt{2}}{4}$,$1+\frac{\sqrt{2}}{4}$],
此时m∈($\frac{1}{2}$,1],
综上所述,m的取值范围是($\frac{1}{2}$,1],
故选:D.
点评 本题考查的知识点是分段函数的应用,是分段函数,分式不等式与二次不等式的综合应用,难度中档.

练习册系列答案
相关题目
4.下面四个图象中,有一个是函数f(x)=$\frac{1}{3}$x3+ax2+(a2-1)x+1(a∈R)的导函数y=f'(x)的图象,则f(-1)等于( )
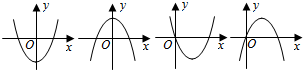
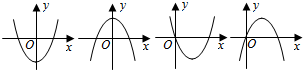
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{5}{3}$ | D. | -$\frac{1}{3}$或$\frac{5}{3}$ |