题目内容
19.已知F是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的一个焦点,B是虚轴的一个端点,线段BF与双曲线相交于D,且$\overrightarrow{BF}=2\overrightarrow{BD}$,则双曲线的离心率为$\sqrt{5}$.分析 利用右焦点为F(c,0),点B(0,b),线段BF与双曲线相交于D,且$\overrightarrow{BF}=2\overrightarrow{BD}$,确定D的坐标,代入双曲线方程,化简可求双曲线的离心率.
解答 解:设D(x,y),
∵右焦点为F(c,0),点B(0,b),线段BF与双曲线相交于D,且$\overrightarrow{BF}=2\overrightarrow{BD}$,
∴x=$\frac{c}{2}$,y=$\frac{b}{2}$,
代入双曲线方程,可得$\frac{\frac{{c}^{2}}{4}}{{a}^{2}}-\frac{\frac{{b}^{2}}{4}}{{b}^{2}}=1$
∴e=$\frac{c}{a}$=$\sqrt{5}$.
故答案为:$\sqrt{5}$.
点评 本题考查向量知识的运用,考查双曲线的离心率,利用向量知识确定D的坐标是关键.

练习册系列答案
相关题目
9.已知函数f(x)=sin(ωx+$\frac{π}{3}$),ω>0,f($\frac{π}{6}$)=f($\frac{π}{3}$),f(x)在区间($\frac{π}{6}$,$\frac{π}{3}$)有最小值无最大值,则?的值为( )
| A. | $\frac{14}{3}$ | B. | $\frac{13}{3}$ | C. | $\frac{3}{14}$ | D. | $\frac{3}{13}$ |
14.已知实数x、y满足$\left\{\begin{array}{l}{x≥1}\\{y≥0}\\{x-y≥0}\end{array}\right.$ 则z=$\frac{y-1}{x}$的取值范围是( )
| A. | [-1,0] | B. | [-1,1) | C. | (-∞,0] | D. | [-1,+∞) |
4.下面四个图象中,有一个是函数f(x)=$\frac{1}{3}$x3+ax2+(a2-1)x+1(a∈R)的导函数y=f'(x)的图象,则f(-1)等于( )
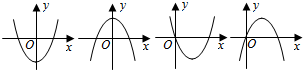
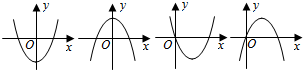
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{5}{3}$ | D. | -$\frac{1}{3}$或$\frac{5}{3}$ |