题目内容
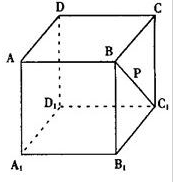 如图点P在正方体ABCD-A1B1C1D1的面对角线BC1上运动,则下列命题:
如图点P在正方体ABCD-A1B1C1D1的面对角线BC1上运动,则下列命题:①DP⊥BC1;
②三棱锥A-D1PC的体积不变;
③面PDB1⊥面ACD1;
④A1P∥面ACD1.
其中正确命题的序号是
考点:直线与平面平行的判定,棱柱、棱锥、棱台的体积,平面与平面垂直的判定
专题:空间位置关系与距离
分析:利用正方体的性质结合空间线面位置关系求解.
解答:
 解:对于①,由于DC⊥平面BCB1C1,所以DC⊥BC1,
解:对于①,由于DC⊥平面BCB1C1,所以DC⊥BC1,
若DP⊥BC1,则BC1⊥平面DCP,
BC1⊥PC,则P为中点,与P为动点矛盾,故①错误;
对于②,由题意知AD1∥BC1,从而BC1∥平面AD1C,
故BC1上任意一点到平面AD1C的距离均相等,
所以以P为顶点,平面AD1C为底面,则三棱锥A-D1PC的体积不变,故②正确;
对于③,连接DB1,由DB1⊥AC且DB1⊥AD1,
可得DB1⊥面ACD1,从而由面面垂直的判定知,故③正确.
对于④,连接A1B,A1C1,A1C1∥AD1且相等,由于①知:AD1∥BC1,
所以BA1C1∥面ACD1,从而由线面平行的定义可得,故④正确;
故答案为:②③④.
 解:对于①,由于DC⊥平面BCB1C1,所以DC⊥BC1,
解:对于①,由于DC⊥平面BCB1C1,所以DC⊥BC1,若DP⊥BC1,则BC1⊥平面DCP,
BC1⊥PC,则P为中点,与P为动点矛盾,故①错误;
对于②,由题意知AD1∥BC1,从而BC1∥平面AD1C,
故BC1上任意一点到平面AD1C的距离均相等,
所以以P为顶点,平面AD1C为底面,则三棱锥A-D1PC的体积不变,故②正确;
对于③,连接DB1,由DB1⊥AC且DB1⊥AD1,
可得DB1⊥面ACD1,从而由面面垂直的判定知,故③正确.
对于④,连接A1B,A1C1,A1C1∥AD1且相等,由于①知:AD1∥BC1,
所以BA1C1∥面ACD1,从而由线面平行的定义可得,故④正确;
故答案为:②③④.
点评:本题考查命题真假的判断,解题时要注意三棱锥体积求法中的等体积法、线面平行、垂直的判定,要注意使用转化的思想.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
若两个函数的图象经过若干次平移后能够重合,则称这两个函数为“同形”函数.给出下列三个函数:f1(x)=sinx+cosx,f2(x)=
sinx+
,f3(x)=sinx,试写出一对“同形”函数是 .
| 2 |
| 2 |
已知等差数列{an}的前n项和为Sn,且a2=4,S2=6,若bn=
,则数列{bn}的前n项和Tn为( )
| 1 |
| Sn |
A、
| ||
B、
| ||
C、
| ||
D、
|
正方形ABCD的边长为4,点E在CD上,且DE:EC=1:3,F为AD的中点,则
•
=( )
| AE |
| BF |
| A、-4 | B、8 | C、4 | D、12 |
化简sin(α-β)cosβ+cos(α-β)sinβ的结果为( )
| A、1 | B、sinα |
| C、cosα | D、sinαcosβ |