题目内容
已知函数f(x)=
x2+
x,数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)均在函数y=f(x)的图象上.
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)若函数g(x)=
,令bn=g(
)(n∈N*)求数列{bn}的前2014项的和T2014.
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)若函数g(x)=
| 4x |
| 4x+2 |
| an |
| 2015 |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由于点(n,Sn)在f(x)的图象上,可得Sn=
n2+
n,利用“当n≥2时,an=Sn-Sn-1;当n=1时,a1=S1,”即可得出;
(2)由于g(x)=
,且g(x)+g(1-x)=1,由(1)知an=n,可得bn=g(
),即可得出.
| 1 |
| 2 |
| 1 |
| 2 |
(2)由于g(x)=
| 4x |
| 4x+2 |
| n |
| 2015 |
解答:
解:(1)∵点(n,Sn)在f(x)的图象上,
∴Sn=
n2+
n,
当n≥2时,an=Sn-Sn-1=n;
当n=1时,a1=S1=1,适合上式,
∴an=n(n∈N*).
(2)∵g(x)=
,且g(x)+g(1-x)=1,
由(1)知an=n,
∴bn=g(
),
∴T2014=b1+b2+…+b2014=g(
)+g(
)+…+g(
)…①
T2014=b2014+b2013+…+b1=g(
)+g(
)+…+g(
)…②
①+②得2T2014=2014(g(
)+g(
))=2014,
∴T2014=1007.
∴Sn=
| 1 |
| 2 |
| 1 |
| 2 |
当n≥2时,an=Sn-Sn-1=n;
当n=1时,a1=S1=1,适合上式,
∴an=n(n∈N*).
(2)∵g(x)=
| 4x |
| 4x+2 |
由(1)知an=n,
∴bn=g(
| n |
| 2015 |
∴T2014=b1+b2+…+b2014=g(
| 1 |
| 2015 |
| 2 |
| 2015 |
| 2014 |
| 2015 |
T2014=b2014+b2013+…+b1=g(
| 2014 |
| 2015 |
| 2013 |
| 2015 |
| 1 |
| 2015 |
①+②得2T2014=2014(g(
| 1 |
| 2015 |
| 2014 |
| 2015 |
∴T2014=1007.
点评:本题考查了递推式的应用、函数的性质、“倒序相加法”,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
若直线(1+a)x+y-1=0与圆x2+y2+4x=0相切,则a的值为( )
| A、1或-1 | ||||
B、
| ||||
| C、1 | ||||
D、-
|
函数y=1+
的零点是( )
| 1 |
| x |
| A、(-1,0) | B、x=-1 |
| C、x=1 | D、x=0 |
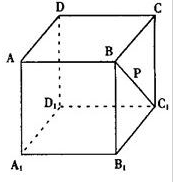 如图点P在正方体ABCD-A1B1C1D1的面对角线BC1上运动,则下列命题:
如图点P在正方体ABCD-A1B1C1D1的面对角线BC1上运动,则下列命题: