题目内容
已知a1=1,(n+1)an+1=nan(n∈N*),求an.
考点:数列递推式
专题:等差数列与等比数列
分析:由已知得
=
,由此利用累乘法能求出结果.
| an+1 |
| an |
| n |
| n+1 |
解答:
解:∵a1=1,(n+1)an+1=nan(n∈N*),
∴
=
,
∴an=a1×
×
×…×
=1×
×
×…×
=
.
∴
| an+1 |
| an |
| n |
| n+1 |
∴an=a1×
| a2 |
| a1 |
| a3 |
| a2 |
| an |
| an-1 |
=1×
| 1 |
| 2 |
| 2 |
| 3 |
| n-1 |
| n |
=
| 1 |
| n |
点评:本题考查数列的通项公式的求法,是基础题,解题时要认真审题,注意累乘法的合理运用.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
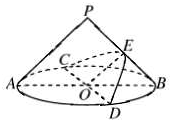 如图,在底面半径和高均为1的圆锥中,AB、CD是底面圆O的两条互相垂直的直径,E是母线PB的中点,已知过CD与E的平面与圆锥侧面的交线是以E为顶点的抛物线的一部分,则该抛物线的焦点到圆锥顶点P的距离为( )
如图,在底面半径和高均为1的圆锥中,AB、CD是底面圆O的两条互相垂直的直径,E是母线PB的中点,已知过CD与E的平面与圆锥侧面的交线是以E为顶点的抛物线的一部分,则该抛物线的焦点到圆锥顶点P的距离为( )| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
已知x,y满足约束条件
,则z=2x-y的最大值为( )
|
| A、-3 | B、1 | C、13 | D、15 |
已知实数x,y满足不等式
,则
的取值范围是( )
|
| 2x3+y3 |
| x2y |
A、[2
| ||||
B、[
| ||||
C、[3,
| ||||
D、[3,
|
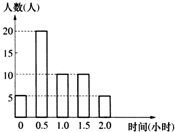 某校为了了解学生的课外阅读情况,随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,结果用下面的条形图表示.根据条形图可得这50名学生这一天平均的课外阅读时间为
某校为了了解学生的课外阅读情况,随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,结果用下面的条形图表示.根据条形图可得这50名学生这一天平均的课外阅读时间为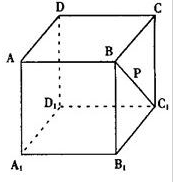 如图点P在正方体ABCD-A1B1C1D1的面对角线BC1上运动,则下列命题:
如图点P在正方体ABCD-A1B1C1D1的面对角线BC1上运动,则下列命题: