题目内容
设∫f（x）dx=x2e2x+C，求f（x）．
考点：微积分基本定理
专题：导数的综合应用
分析：利用积分和求导的逆运算关系求f（x）．
解答：
解：因为∫f（x）dx=x2e2x+C，所以（∫f（x）dx）′=（x2e2x+C）′=2xe2x+2x2e2x=2xe2x（1+x）=f（x）．
点评：本题考查了积分与求导的逆运算关系的运用，属于基础题．
练习册系列答案
相关题目
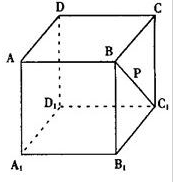如图点P在正方体ABCD-A1B1C1D1的面对角线BC1上运动，则下列命题：