题目内容

若两个函数的图象经过若干次平移后能够重合，则称这两个函数为“同形”函数．给出下列三个函数：f1（x）=sinx+cosx，f2（x）=
2
sinx+
2
，f3（x）=sinx，试写出一对“同形”函数是
 
．
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：利用三角函数的平移的法则可知函数f1（x）=
2
sin（x+
π
4
）先向右平移
π
4
个单位得f1（x）=
2
sinx，再向上平移
2
个单位得到函数f（x）=
2
sinx+
2
，这一函数正好与②中的函数重合．
解答： 解：①f1（x）=sinx+cosx=
2
sin（x+
π
4
）先向右平移
π
4
个单位得f1（x）=
2
sinx，再向上平移
2
个单位得到函数②f2（x）=
2
sinx+
2
，这一函数正好与②中的函数重合．
故答案为：f1（x）=sinx+cosx，f2（x）=
2
sinx+
2
．
点评：本题主要考查了三角函数的图象的变换．考查了学生对三角函数基础知识的掌握的熟练程度．
练习册系列答案
相关题目
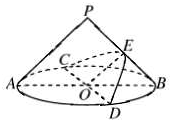如图，在底面半径和高均为1的圆锥中，AB、CD是底面圆O的两条互相垂直的直径，E是母线PB的中点，已知过CD与E的平面与圆锥侧面的交线是以E为顶点的抛物线的一部分，则该抛物线的焦点到圆锥顶点P的距离为（　　）
A、1
B、
2
4
C、
6
2
D、
10
4
将一长为18cm的线段随机地分成三段，则这三段能组成一个三角形的概率是多少？
已知过椭圆
x2
4
+
y2
3
=1右焦点作倾斜角为45°的弦AB，求AB的长．
已知数列{an}的前n项和为Sn，且满足Sn=2an-n（n∈N+）．
（1）求数列{an}的通项公式；
（2）若bn=（2n+1）（an+1），数列{bn}的前n项为Tn，求满足不等式
Tn-2
2n-1
≥2的最小的n的值．
已知椭圆C的焦点F1（0，-4）和F2（0，4），长轴长10，又双曲线D与椭圆C共焦点，它们的离心率之和为
14
5
，试求：
（1）椭圆的方程；
（2）双曲线的方程．
已知函数f（x）=-x2+5x-6，求：
（1）y=f（x）的图象与x轴交点的横坐标x的集合；
（2）y=f（x）的图象在x轴上方时横坐标x的集合；
（3）y=f（x）的图象恒在直线y=a+1下方时横坐标x的集合．
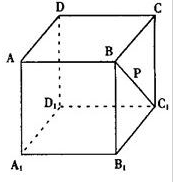如图点P在正方体ABCD-A1B1C1D1的面对角线BC1上运动，则下列命题：
①DP⊥BC1；
②三棱锥A-D1PC的体积不变；
③面PDB1⊥面ACD1；
④A1P∥面ACD1．
其中正确命题的序号是
 
．
某校从参加考试的学生中抽出40名学生，将其成绩（均为整数）分成六组[40，50），[50，60）…[90，100]后画出如下部分频率分布直方图．观察图形的信息，回答下列问题：

（Ⅰ）求成绩落在[80，90）上的频率，并补全这个频率分布直方图；
（Ⅱ）估计这次考试的及格率（60分及以上为及格）和平均分；
（Ⅲ）从成绩是80分以上（包括80分）的学生中选两人，求他们在同一分数段的概率．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网