题目内容
化简sin(α-β)cosβ+cos(α-β)sinβ的结果为( )
| A、1 | B、sinα |
| C、cosα | D、sinαcosβ |
考点:两角和与差的正弦函数,两角和与差的余弦函数
专题:计算题,三角函数的求值
分析:逆用两角和的正弦公式,注意将α-β看作一个角,即可化简得到.
解答:
解:由两角和的正弦公式,可得
sin(α-β)cosβ+cos(α-β)sinβ
=sin[(α-β)+β]=sinα.
故选B.
sin(α-β)cosβ+cos(α-β)sinβ
=sin[(α-β)+β]=sinα.
故选B.
点评:本题考查两角和的正弦公式,注意逆用公式,以及整体思想,考查运算能力,属于基础题.

练习册系列答案
相关题目
若直线(1+a)x+y-1=0与圆x2+y2+4x=0相切,则a的值为( )
| A、1或-1 | ||||
B、
| ||||
| C、1 | ||||
D、-
|
下列函数中,增长速度最快的是( )
| A、y=20x |
| B、y=x20 |
| C、y=log20x |
| D、y=20x |
函数y=1+
的零点是( )
| 1 |
| x |
| A、(-1,0) | B、x=-1 |
| C、x=1 | D、x=0 |
直线x+7=0的倾斜角为( )
| A、0 | ||
B、
| ||
| C、π | ||
| D、不存在 |
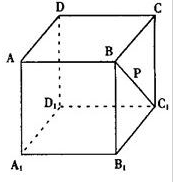 如图点P在正方体ABCD-A1B1C1D1的面对角线BC1上运动,则下列命题:
如图点P在正方体ABCD-A1B1C1D1的面对角线BC1上运动,则下列命题: