题目内容
正方形ABCD的边长为4，点E在CD上，且DE：EC=1：3，F为AD的中点，则
•
=（ ）
| AE |
| BF |
| A、-4 | B、8 | C、4 | D、12 |
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：运用向量加法的三角形法则和向量的数量积的定义和性质，化简即可得到所求值．
解答：
解：
•
=（
+
）•（
+
）
=（
+
）•（-
+
）
=（
+
）•（-
+
）
=
2-
2-
•
=
×16-
×16=4．
故选C．
| AE |
| BF |
| AD |
| DE |
| BA |
| AF |
=（
| AD |
| 1 |
| 4 |
| DC |
| AB |
| 1 |
| 2 |
| AD |
=（
| AD |
| 1 |
| 4 |
| AB |
| AB |
| 1 |
| 2 |
| AD |
=
| 1 |
| 2 |
| AD |
| 1 |
| 4 |
| AB |
| 7 |
| 8 |
| AB |
| AD |
=
| 1 |
| 2 |
| 1 |
| 4 |
故选C．
点评：本题考查平面向量的数量积的定义和性质，考查向量的加减运算和数量积的运算，属于中档题．
练习册系列答案
相关题目
已知实数x，y满足不等式
，则
的取值范围是（ ）
|
| 2x3+y3 |
| x2y |
A、[2
| ||||
B、[
| ||||
C、[3，
| ||||
D、[3，
|
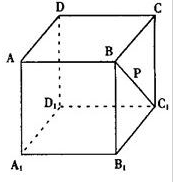如图点P在正方体ABCD-A1B1C1D1的面对角线BC1上运动，则下列命题：下列函数中，增长速度最快的是（ ）
| A、y=20x |
| B、y=x20 |
| C、y=log20x |
| D、y=20x |