题目内容
11．6个人排成一排，其中甲不能排在两端的排法数有（ ）| A． | 120种 | B． | 240种 | C． | 480种 | D． | 600种 |
分析 根据题意，分2步进行分析：1、分析甲的排法，易得甲甲可以排在中间的4个位置，有4种情况，2、将剩余的5人全排列，安排在其他5个位置，由排列数公式可得其情况数目，由分步计数原理计算可得答案．
解答 解：根据题意，分2步进行分析：
1、甲不能排在两端，则甲可以排在中间的4个位置，有4种情况，
2、将剩余的5人全排列，安排在其他5个位置，有A55=120种情况，
则甲不能排在两端的排法有4×120=480种；
故选：C．
点评 本题考查排列、组合的运用，对于受到限制的元素，一般要优先分析．
练习册系列答案
全能练考卷系列答案
相关题目
2．设函数f（x）=x2-4x+3，g（x）=3x-2，集合M={x∈R|f（g（x））＞0}，N={x∈R|g（x）＜2}，则M∩N为（ ）
| A． | （1，+∞） | B． | （0，1） | C． | （-1，1） | D． | （-∞，1） |
3．
如图是一个水平放置的直观图，它是一个底角为45°，腰和上底均为1的等腰梯形，那么原平面图形的面积为（ ）
如图是一个水平放置的直观图，它是一个底角为45°，腰和上底均为1的等腰梯形，那么原平面图形的面积为（ ）| A． | 2+$\sqrt{2}$ | B． | $\frac{{1+\sqrt{2}}}{2}$ | C． | $\frac{{2+\sqrt{2}}}{2}$ | D． | 1+$\sqrt{2}$ |
20．一只昆虫在边长分别为6，8，10的三角形区域内随机爬行，则其到三角形任一顶点的距离不小于2的概率为（ ）
| A． | 1-$\frac{π}{12}$ | B． | 1-$\frac{π}{10}$ | C． | 1-$\frac{π}{6}$ | D． | 1-$\frac{π}{24}$ |
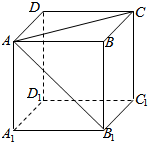在如图所示的正方体ABCD-A1B1C1D1中，求：