题目内容
1.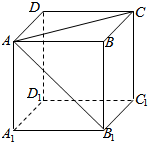 在如图所示的正方体ABCD-A1B1C1D1中,求:
在如图所示的正方体ABCD-A1B1C1D1中,求:(1)AA1与C1D1所成的角;
(2)AB1与C1D1所成的角;
(3)AC与A1B所成的角.
分析 (1)容易看出∠AA1B1为AA1与C1D1所成角,且该角为90°;
(2)可以看出∠AB1A1为AB1与C1D1所成角,且该角为45°;
(3)连接A1C1,BC1,从而∠BA1C1是AC与A1B所成的角,并且可看出该角为60°.
解答  解:(1)A1B1∥C1D1;
解:(1)A1B1∥C1D1;
∴∠AA1B1为异面直线AA1与C1D1所成的角,且∠AA1B1=90°;
∴AA1与C1D1所成的角为90°;
(2)A1B1∥C1D1;
∴∠AB1A1为异面直线AB1与C1D1所成的角;
∴异面直线AB1与C1D1所成的角为45°;
(3)如图,连接A1C1,BC1,则:A1C1∥AC;
∴∠BA1C1是AC与A1B所成角;
△A1BC1为等边三角形;
∴∠BA1C1=60°;
∴AC与A1B所成角为60°.
点评 考查异面直线所成角的定义及求法,正方体的概念及正方体面对角线相等.

练习册系列答案
相关题目
11.6个人排成一排,其中甲不能排在两端的排法数有( )
| A. | 120种 | B. | 240种 | C. | 480种 | D. | 600种 |
9.在正方体ABCD-A1B1C1D1中任取一点P,则点P在三棱锥B1-ABC的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |
13.若指数函数f(x)=(a2-1)x在(-∞,+∞)上是减函数,则a的取值范围是( )
| A. | |a|>1 | B. | |a||<$\sqrt{2}$ | C. | |a|>$\sqrt{2}$ | D. | 1<|a|<$\sqrt{2}$ |
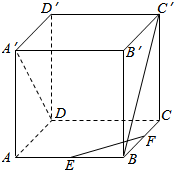 如图,正方体ABCD-A′B′C′D′的棱长为a,E,F分别是棱AB,BC的中点,求:
如图,正方体ABCD-A′B′C′D′的棱长为a,E,F分别是棱AB,BC的中点,求: