题目内容
1.在极坐标系中,极点为O,已知P1(1+$\sqrt{2}$,0),P2(1+$\sqrt{2}$,$\frac{π}{2}$),曲线C:p=2$\sqrt{2}$sinθ.(1)求直线P1P2的极坐标方程;
(2)记直线P1P2与曲线C交与A,B两点,求∠AOB的大小.
分析 (1)由P1(1+$\sqrt{2}$,0),P2(1+$\sqrt{2}$,$\frac{π}{2}$),利用$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$,可得直角坐标P1,P2.可得直角坐标方程,再化为极坐标方程即可.
(2)曲线C:ρ=2$\sqrt{2}$sinθ,化为${ρ}^{2}=2\sqrt{2}ρsinθ$,可得直角坐标方程为:${x}^{2}+(y-\sqrt{2})^{2}$=2.曲线C是以M$(0,\sqrt{2})$为圆心,$\sqrt{2}$为半径的圆.过点M作MQ⊥AB与点Q,连接MA,MB,MP2,MO.利用斜率与直角三角形的边角关系可得:∠AMQ,利用∠AOB=$\frac{1}{2}$∠AMB=∠AMQ即可得出.
解答 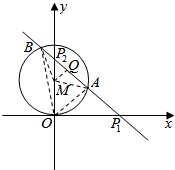 解:(1)由P1(1+$\sqrt{2}$,0),P2(1+$\sqrt{2}$,$\frac{π}{2}$),利用$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$,可得:P1(1+$\sqrt{2}$,0),P2(0,1+$\sqrt{2}$).
解:(1)由P1(1+$\sqrt{2}$,0),P2(1+$\sqrt{2}$,$\frac{π}{2}$),利用$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$,可得:P1(1+$\sqrt{2}$,0),P2(0,1+$\sqrt{2}$).
∴直线P1P2的直角坐标方程为:$\frac{x}{1+\sqrt{2}}+\frac{y}{1+\sqrt{2}}$=1,化为x+y=1+$\sqrt{2}$.
∴极坐标方程为:ρcosθ+ρsinθ=1+$\sqrt{2}$.
(2)曲线C:ρ=2$\sqrt{2}$sinθ,化为${ρ}^{2}=2\sqrt{2}ρsinθ$,
可得直角坐标方程为:x2+y2=2$\sqrt{2}$y,
配方为${x}^{2}+(y-\sqrt{2})^{2}$=2.
∴曲线C是以M$(0,\sqrt{2})$为圆心,$\sqrt{2}$为半径的圆.
过点M作MQ⊥AB与点Q,连接MA,MB,MP2,MO.
在Rt△MQP2中,∠MP2Q=∠OP2P1=45°,
∴|MP2|=|OP2|-|OM|=1.
故|MQ|=$\frac{\sqrt{2}}{2}$|MP2|=$\frac{\sqrt{2}}{2}$.
在Rt△MQA中,|MQ|=$\frac{1}{2}$|AM|,
故∠AMQ=60°,
因此∠AOB=$\frac{1}{2}$∠AMB=∠AMQ=60°.
点评 本题考查了极坐标方程与直角坐标方程互化的方法、直线与圆相交问题、垂经定理、圆心角与圆周角的关系,考查了推理能力与计算能力,属于中档题.

 优生乐园系列答案
优生乐园系列答案| A. | 120种 | B. | 240种 | C. | 480种 | D. | 600种 |