题目内容
19.抛物线y2=8x上一点P到焦点的距离为6,在y轴上的射影为Q,O为原点,则四边形OFPQ的面积等于12$\sqrt{2}$.分析 先利用抛物线的定义,根据抛物线y2=8x上的点P到焦点F的距离为6,确定点P的横坐标,进而可得P的坐标,即可求得四边形OFPQ的面积.
解答 解:∵抛物线y2=8x上的点P(x,y)到焦点F的距离为6,
∴x+$\frac{p}{2}$=x+2=6,
∴x=4,
抛物线方程为y2=8x
∴x=4时,y=±4$\sqrt{2}$,
∴P的坐标为(4,±4$\sqrt{2}$)
∴四边形OFPQ是一个梯形,其面积为S=$\frac{1}{2}$(2+4)×4$\sqrt{2}$=12$\sqrt{2}$.
故答案为:12$\sqrt{2}$.
点评 本题考查抛物线的定义,考查四边形面积的计算,确定点P的位置是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.6个人排成一排,其中甲不能排在两端的排法数有( )
| A. | 120种 | B. | 240种 | C. | 480种 | D. | 600种 |
9.在正方体ABCD-A1B1C1D1中任取一点P,则点P在三棱锥B1-ABC的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |
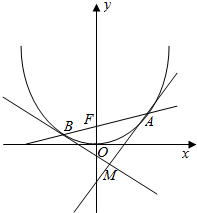 如图所示,已知过抛物线x2=2py(p>0)的焦点F的直线l与抛物线相交于A,B两点
如图所示,已知过抛物线x2=2py(p>0)的焦点F的直线l与抛物线相交于A,B两点