题目内容
20.一只昆虫在边长分别为6,8,10的三角形区域内随机爬行,则其到三角形任一顶点的距离不小于2的概率为( )| A. | 1-$\frac{π}{12}$ | B. | 1-$\frac{π}{10}$ | C. | 1-$\frac{π}{6}$ | D. | 1-$\frac{π}{24}$ |
分析 先求出三角形的面积,再求出据三角形的三顶点距离小于等于2的区域为三个扇形,三个扇形的和是半圆,求出半圆的面积,利用几何概型概率公式求出恰在离三个顶点距离都不小于2的地方的概率.
解答  解:昆虫活动的范围是在三角形的内部,三角形的边长为6,8,10,是直角三角形,
解:昆虫活动的范围是在三角形的内部,三角形的边长为6,8,10,是直角三角形,
∴面积为$\frac{1}{2}×6×8$=24,而“恰在离三个顶点距离都小于2”正好是一个半径为2的半圆,
面积为$\frac{1}{2}$π×22=4π×$\frac{1}{2}$=2π,
∴根据几何概型的概率公式可知其到三角形顶点的距离不小于2的地方的概率为$\frac{2π}{24}$=$\frac{π}{12}$.
故选:A.
点评 本题主要考查几何概型概率公式、三角形的面积公式、圆的面积公式,属于中档题.

练习册系列答案
相关题目
11.6个人排成一排,其中甲不能排在两端的排法数有( )
| A. | 120种 | B. | 240种 | C. | 480种 | D. | 600种 |
9.在正方体ABCD-A1B1C1D1中任取一点P,则点P在三棱锥B1-ABC的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |
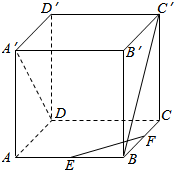 如图,正方体ABCD-A′B′C′D′的棱长为a,E,F分别是棱AB,BC的中点,求:
如图,正方体ABCD-A′B′C′D′的棱长为a,E,F分别是棱AB,BC的中点,求: