题目内容
(2014·成都模拟)已知函数f(x)=x2+ +alnx(x>0).
+alnx(x>0).
(1)若f(x)在[1,+∞)上单调递增,求a的取值范围.
(2)若定义在区间D上的函数y=f(x)对于区间D上的任意两个值x1,x2总有不等式 [f(x1)+f(x2)]≥f
[f(x1)+f(x2)]≥f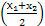 成立,则称函数y=f(x)为区间D上的“凹函数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函数”.试证当a≤0时,f(x)为“凹函数”.
 +alnx(x>0).
+alnx(x>0).(1)若f(x)在[1,+∞)上单调递增,求a的取值范围.
(2)若定义在区间D上的函数y=f(x)对于区间D上的任意两个值x1,x2总有不等式
 [f(x1)+f(x2)]≥f
[f(x1)+f(x2)]≥f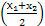 成立,则称函数y=f(x)为区间D上的“凹函数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函数”.试证当a≤0时,f(x)为“凹函数”.(1)a≥0 (2)见解析
(1)由f(x)=x2+ +alnx,
+alnx,
得f′(x)=2x-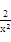 +
+ .
.
因为函数为[1,+∞)上的单调增函数.
则f′(x)≥0在[1,+∞)上恒成立,
即不等式2x-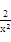 +
+ ≥0在[1,+∞)上恒成立.
≥0在[1,+∞)上恒成立.
即a≥ -2x2在[1,+∞)上恒成立.
-2x2在[1,+∞)上恒成立.
令φ(x)= -2x2,上述问题等价于a≥φ(x)max,而φ(x)=
-2x2,上述问题等价于a≥φ(x)max,而φ(x)= -2x2为[1,+∞)上的减函数,则φ(x)max=φ(1)=0,于是a≥0为所求.
-2x2为[1,+∞)上的减函数,则φ(x)max=φ(1)=0,于是a≥0为所求.
(2)由f(x)=x2+ +alnx得
+alnx得
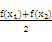 =
= (
(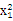 +
+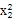 )+
)+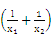 +
+ (lnx1+lnx2)
(lnx1+lnx2)
= (
(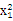 +
+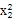 )+
)+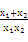 +aln
+aln ,
,
f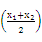 =
=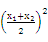 +
+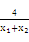 +aln
+aln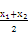 ,
,
而 (
(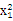 +
+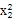 )≥
)≥ [(
[(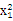 +
+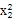 )+2x1x2]=
)+2x1x2]=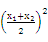 , ①
, ①
又(x1+x2)2=(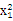 +
+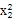 )+2x1x2≥4x1x2,
)+2x1x2≥4x1x2,
所以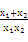 ≥
≥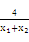 . ②
. ②
因为 ≤
≤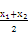 ,所以ln
,所以ln ≤ln
≤ln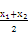 ,
,
因为a≤0,所以aln ≥aln
≥aln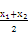 , ③
, ③
由①②③得 (
(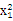 +
+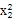 )+
)+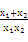 +aln
+aln ≥
≥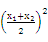 +
+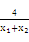 +aln
+aln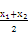 ,
,
即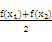 ≥f
≥f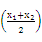 ,
,
从而由凹函数的定义可知a≤0时,函数f(x)为凹函数.
 +alnx,
+alnx,得f′(x)=2x-
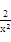 +
+ .
.因为函数为[1,+∞)上的单调增函数.
则f′(x)≥0在[1,+∞)上恒成立,
即不等式2x-
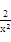 +
+ ≥0在[1,+∞)上恒成立.
≥0在[1,+∞)上恒成立.即a≥
 -2x2在[1,+∞)上恒成立.
-2x2在[1,+∞)上恒成立.令φ(x)=
 -2x2,上述问题等价于a≥φ(x)max,而φ(x)=
-2x2,上述问题等价于a≥φ(x)max,而φ(x)= -2x2为[1,+∞)上的减函数,则φ(x)max=φ(1)=0,于是a≥0为所求.
-2x2为[1,+∞)上的减函数,则φ(x)max=φ(1)=0,于是a≥0为所求.(2)由f(x)=x2+
 +alnx得
+alnx得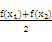 =
= (
(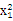 +
+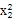 )+
)+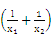 +
+ (lnx1+lnx2)
(lnx1+lnx2)=
 (
(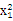 +
+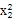 )+
)+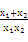 +aln
+aln ,
,f
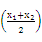 =
=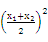 +
+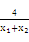 +aln
+aln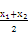 ,
,而
 (
(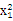 +
+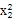 )≥
)≥ [(
[(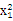 +
+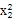 )+2x1x2]=
)+2x1x2]=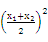 , ①
, ①又(x1+x2)2=(
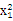 +
+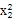 )+2x1x2≥4x1x2,
)+2x1x2≥4x1x2,所以
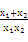 ≥
≥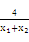 . ②
. ②因为
 ≤
≤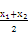 ,所以ln
,所以ln ≤ln
≤ln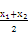 ,
,因为a≤0,所以aln
 ≥aln
≥aln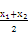 , ③
, ③由①②③得
 (
(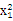 +
+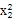 )+
)+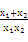 +aln
+aln ≥
≥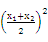 +
+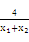 +aln
+aln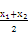 ,
,即
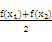 ≥f
≥f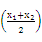 ,
,从而由凹函数的定义可知a≤0时,函数f(x)为凹函数.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案
相关题目
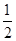 ,-
,-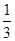 ]上有单调递增区间?
]上有单调递增区间? 在
在 为单调增函数,则实数
为单调增函数,则实数 的取值范围为( )
的取值范围为( )



 满足下列条件:
满足下列条件: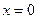 处导数为-1;③在
处导数为-1;③在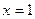 处切线方程为
处切线方程为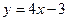 .
.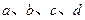 的值;
的值; 表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于
表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于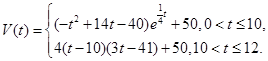
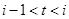 表示第1月份(
表示第1月份( ),同一年内哪几个月份是枯水期?
),同一年内哪几个月份是枯水期?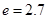 计算).
计算).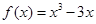 在区间
在区间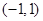 上( )
上( )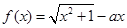
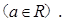
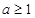 时,函数
时,函数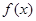 在区间
在区间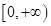 上是单调递减函数;
上是单调递减函数;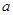 的取值范围,使函数
的取值范围,使函数 都是定义在
都是定义在 上的函数,
上的函数, ,
, ,且
,且 ,
,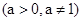 ,
, ,对于数列
,对于数列 ,任取正整数
,任取正整数 ,则前k项和大于
,则前k项和大于 的概率是( )
的概率是( )



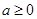 ,函数
,函数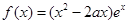 ,若
,若 在
在 上是单调减函数,则
上是单调减函数,则 的取值范围是( )
的取值范围是( )