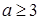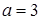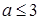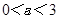题目内容
设f(x)=ln(1+x)-x-ax2.
(1)当x=1时,f(x)取到极值,求a的值;
(2)当a满足什么条件时,f(x)在区间[-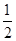 ,-
,-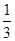 ]上有单调递增区间?
]上有单调递增区间?
(1)当x=1时,f(x)取到极值,求a的值;
(2)当a满足什么条件时,f(x)在区间[-
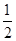 ,-
,-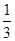 ]上有单调递增区间?
]上有单调递增区间?(1)a=-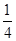 (2)a∈(-1,+∞).
(2)a∈(-1,+∞).
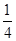 (2)a∈(-1,+∞).
(2)a∈(-1,+∞).解:(1)由题意知,f(x)的定义域为(-1,+∞),
且f′(x)=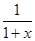 -2ax-1=
-2ax-1=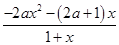 ,
,
由题意得:f′(1)=0,则-2a-2a-1=0,得a=-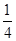 ,
,
又当a=-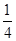 时,f′(x)=
时,f′(x)= =
=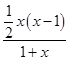 ,
,
当0<x<1时,f′(x)<0;当x>1时,f′(x)>0,
所以f(1)是函数f(x)的极大值,所以a=-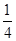 .
.
(2)要使f(x)在区间[-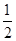 ,-
,-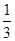 ]上有单调递增区间,
]上有单调递增区间,
即要求f′(x)>0在区间[-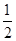 ,-
,-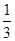 ]上有解,
]上有解,
当-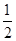 ≤x≤-
≤x≤-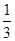 时,
时,
f′(x)>0等价于2ax+(2a+1)>0.
①当a=0时,不等式恒成立;
②当a>0时,得x>-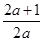 ,
,
此时只要-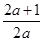 <-
<-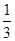 ,
,
解得a>0;
③当a<0时,得x<-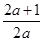 ,
,
此时只要-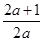 >-
>-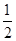 ,
,
解得-1<a<0.
综上所述,a∈(-1,+∞).
且f′(x)=
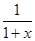 -2ax-1=
-2ax-1=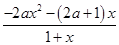 ,
,由题意得:f′(1)=0,则-2a-2a-1=0,得a=-
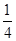 ,
,又当a=-
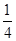 时,f′(x)=
时,f′(x)= =
=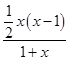 ,
,当0<x<1时,f′(x)<0;当x>1时,f′(x)>0,
所以f(1)是函数f(x)的极大值,所以a=-
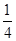 .
.(2)要使f(x)在区间[-
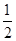 ,-
,-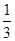 ]上有单调递增区间,
]上有单调递增区间,即要求f′(x)>0在区间[-
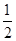 ,-
,-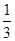 ]上有解,
]上有解,当-
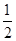 ≤x≤-
≤x≤-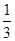 时,
时,f′(x)>0等价于2ax+(2a+1)>0.
①当a=0时,不等式恒成立;
②当a>0时,得x>-
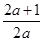 ,
,此时只要-
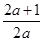 <-
<-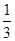 ,
,解得a>0;
③当a<0时,得x<-
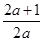 ,
,此时只要-
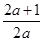 >-
>-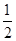 ,
,解得-1<a<0.
综上所述,a∈(-1,+∞).

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
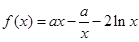 .
.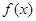 在
在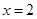 时有极值,求实数
时有极值,求实数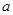 的值和
的值和 +alnx(x>0).
+alnx(x>0). [f(x1)+f(x2)]≥f
[f(x1)+f(x2)]≥f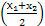 成立,则称函数y=f(x)为区间D上的“凹函数”.试证当a≤0时,f(x)为“凹函数”.
成立,则称函数y=f(x)为区间D上的“凹函数”.试证当a≤0时,f(x)为“凹函数”. ,若
,若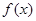 存在唯一的零点
存在唯一的零点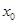 ,且
,且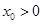 ,则
,则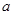 的取值范围是
的取值范围是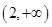

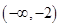
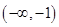
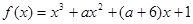 有极大值和极小值,则
有极大值和极小值,则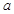 的取值范围为( )
的取值范围为( )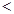
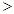 2
2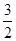 )
)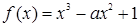 在
在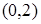 上单调递减,则实数
上单调递减,则实数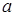 的取值范围为( )
的取值范围为( )