题目内容
2.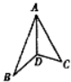 在正三角形ABC中,AD⊥BC于D,沿AD折成二面角B-AD-C后,BC=$\frac{1}{2}$AB,这时二面角B-AD-C的大小为60°.
在正三角形ABC中,AD⊥BC于D,沿AD折成二面角B-AD-C后,BC=$\frac{1}{2}$AB,这时二面角B-AD-C的大小为60°.
分析 根据已知条件能够说明∠BDC为二面角B-AD-C的平面角,连接BC,从而容易说明△BCD为正三角形,从而得出二面角B-AD-C的大小为60°.
解答 解:根据已知条件知D为正三角形ABC边BC中点,且BD⊥AD,CD⊥AD;
∴∠BDC为二面角B-AD-C的平面角,连接BC;
由BC=$\frac{1}{2}AB$=BD=CD得△BCD为正三角形;
∴∠BDC=60°;
∴二面角B-AD-C的大小为60°.
故答案为:60°.
点评 考查二面角平面角的概念及求法,弄清图形折叠前后的变化,等边三角形的高线也是中线.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
5.若全集U=R,集合A={x|-7<2x+3<7},B={x|y=log2(x2-4)},则CU(A∩B)=( )
| A. | {x|x<-5或x>-2} | B. | {x|x≤-5或x≥-2} | C. | {x|x≤-3或x≥-1} | D. | {x|x<-3或x>-1} |
7.复数z满足(z-2i)(1+i)=|1+$\sqrt{3}i$|(i为虚数单位),则复数z=( )
| A. | 1+i | B. | 1-i | C. | 1 | D. | -1 |
14.若复数$\frac{m+i}{2-i}$为纯虚数,则实数m=( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |