题目内容
7.复数z满足(z-2i)(1+i)=|1+$\sqrt{3}i$|(i为虚数单位),则复数z=( )| A. | 1+i | B. | 1-i | C. | 1 | D. | -1 |
分析 求出复数的模,利用复数的除法运算法则,化简求解即可.
解答 解:复数z满足(z-2i)(1+i)=|1+$\sqrt{3}i$|=2,
z=$\frac{2}{1+i}+2i$=$\frac{2(1-i)}{(1+i)(1-i)}+2i$=1+i.
故选:A.
点评 本题考查复数的基本运算,复数的模的求法,考查计算能力.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
10.已知命题p:“将函数y=sin(2x+θ)的图象沿x轴向右平移$\frac{π}{16}$个单位后,得到一个关于y轴对称的图象”,命题q“θ=kπ+$\frac{5π}{8}$(k∈Z)“,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
19.直线l过抛物线C:y2=4x的焦点,且与抛物线C交于A、B两点,过点A、B分别向抛物线的准线作垂线,垂足分别为P、Q,则四边形APQB的面积的最小值为( )
| A. | 6 | B. | 8 | C. | $8\sqrt{2}$ | D. | $10\sqrt{2}$ |
16. 对某校高二年级学生暑期参加社会实践次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社会实践的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如图:
对某校高二年级学生暑期参加社会实践次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社会实践的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如图:
(1)求出表中M,p及图中a的值;
(2)在所取样本中,从参加社会实践的次数不少于20次的学生中任选3人,记参加社会实践次数在区间[25,30)内的人数为X,求X的分布列和期望.
 对某校高二年级学生暑期参加社会实践次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社会实践的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如图:
对某校高二年级学生暑期参加社会实践次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社会实践的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如图:| 分组 | 频数 | 频率 |
| [10,15) | 20 | 0.25 |
| [15,20) | 48 | n |
| [20,25) | m | p |
| [25,30) | 4 | 0.05 |
| 合计 | M | 1 |
(2)在所取样本中,从参加社会实践的次数不少于20次的学生中任选3人,记参加社会实践次数在区间[25,30)内的人数为X,求X的分布列和期望.
17.设i为虚数单位,则复数z=$\frac{{{i^{2015}}}}{{1-{i^{2015}}}}$在复平面中对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图:我国海监船沿东西方向的海岸线l上的M、N处停泊着我国渔民的捕鱼船,MN=1km,我国海监船在点M的正东方向30km的点O处,观测到一日系船正匀速直线航向我国海域,当该日系船位于点O的北偏东30°方向上的A处(OA=20$\sqrt{3}$km)时,我方开始向日方喊话,但该日系船仍匀速航行,40min后,又测该日系船位于点O的正北方向上的点B处,且OB=20km.(参考数据:$\sqrt{3}$≈1.732)
如图:我国海监船沿东西方向的海岸线l上的M、N处停泊着我国渔民的捕鱼船,MN=1km,我国海监船在点M的正东方向30km的点O处,观测到一日系船正匀速直线航向我国海域,当该日系船位于点O的北偏东30°方向上的A处(OA=20$\sqrt{3}$km)时,我方开始向日方喊话,但该日系船仍匀速航行,40min后,又测该日系船位于点O的正北方向上的点B处,且OB=20km.(参考数据:$\sqrt{3}$≈1.732)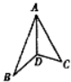 在正三角形ABC中,AD⊥BC于D,沿AD折成二面角B-AD-C后,BC=$\frac{1}{2}$AB,这时二面角B-AD-C的大小为60°.
在正三角形ABC中,AD⊥BC于D,沿AD折成二面角B-AD-C后,BC=$\frac{1}{2}$AB,这时二面角B-AD-C的大小为60°.