题目内容
10.设X~N(6,1),求P(4<X≤5).分析 根据变量符合正态分布,和所给的μ和σ的值,根据3σ原则,得到P(4<X≤8)=0.9544,P(5<X≤7)=0.6826,两个式子相减,根据对称性得到结果.
解答 解:由已知μ=6,σ=1
∵P(μ-2σ<X≤μ+2σ)=0.9544,P(μ-σ<X≤μ+σ)=0.6826,μ=6,σ=1,
∴P(4<X≤8)=0.9544,P(5<X≤7)=0.6826,
∴P(4<X≤8)-P(5<X≤7)=0.9544-0.6826=0.2718,
∴P(4<X≤5)=$\frac{1}{2}$×0.2718=0.1359.
点评 本题考查正态分布曲线的特点及曲线所表示的意义,考查正态分布中两个量μ和σ的应用,考查曲线的对称性,属于基础题.

练习册系列答案
相关题目
9.已知某高级中学高三学生有2000名,在第一次模拟考试中数学成绩ξ服从正态分布N(120,σ2),已知P(100<?<120)=0.45.若学校教研室欲按分层抽样的方式从中抽出100份试卷进行分析研究,则应从140分以上的试卷中抽( )
| A. | 4份 | B. | 5份 | C. | 8份 | D. | 10份 |
6.某城市随机监测一年内100天的空气质量PM2.5的数据API,结果统计如下:
(1)若将API值低于150的天气视为“好天”,并将频率视为概率,根据上述表格,预测今年高考6月7日、8日两天连续出现“好天”的概率;
(2)API值对部分生产企业有着重大的影响,假设某企业的日利润f(x)与API值x的函数关系为:f(x)=$\left\{\begin{array}{l}40(x≤150)\\ 15(x>150)\end{array}$(单位;万元),利用分层抽样的方式从监测的100天中选出5天,再从这5天中任取3天计算企业利润之和,求利润之和小于80万元的概率.
| API | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,+∞) |
| 天数 | 6 | 12 | 22 | 30 | 14 | 16 |
(2)API值对部分生产企业有着重大的影响,假设某企业的日利润f(x)与API值x的函数关系为:f(x)=$\left\{\begin{array}{l}40(x≤150)\\ 15(x>150)\end{array}$(单位;万元),利用分层抽样的方式从监测的100天中选出5天,再从这5天中任取3天计算企业利润之和,求利润之和小于80万元的概率.
 如图,在棱长为1的正四面体A-BCD中,平面α与棱AB,AD,CD,BC分别交于点E,F,G,H,则四边形EFGH周长的最小值为2.
如图,在棱长为1的正四面体A-BCD中,平面α与棱AB,AD,CD,BC分别交于点E,F,G,H,则四边形EFGH周长的最小值为2.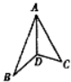 在正三角形ABC中,AD⊥BC于D,沿AD折成二面角B-AD-C后,BC=$\frac{1}{2}$AB,这时二面角B-AD-C的大小为60°.
在正三角形ABC中,AD⊥BC于D,沿AD折成二面角B-AD-C后,BC=$\frac{1}{2}$AB,这时二面角B-AD-C的大小为60°.