题目内容
已知函数f(x)=1+x-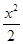 +
+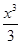 -
-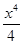 +…+
+…+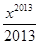 ,则下列结论正确的是( )
,则下列结论正确的是( )
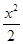 +
+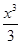 -
-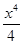 +…+
+…+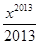 ,则下列结论正确的是( )
,则下列结论正确的是( )| A.f(x)在(0,1)上恰有一个零点 |
| B.f(x)在(0,1)上恰有两个零点 |
| C.f(x)在(-1,0)上恰有一个零点 |
| D.f(x)在(-1,0)上恰有两个零点 |
C
函数的导数为f′(x)=1-x+x2-…+x2012=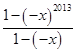 =
=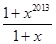 .当x∈(0,1)时,f′(x)>0,此时函数单调递增.当x∈(-1,0)时,f′(x)>0,此时函数单调递增.因为f(0)=1>0,所以函数在(0,1)上没有零点.又f(-1)=1-1-
.当x∈(0,1)时,f′(x)>0,此时函数单调递增.当x∈(-1,0)时,f′(x)>0,此时函数单调递增.因为f(0)=1>0,所以函数在(0,1)上没有零点.又f(-1)=1-1-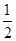 -
-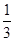 -…-
-…-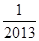 <0,所以函数在(-1,0)上有且只有一个零点,所以选C.
<0,所以函数在(-1,0)上有且只有一个零点,所以选C.
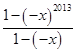 =
=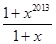 .当x∈(0,1)时,f′(x)>0,此时函数单调递增.当x∈(-1,0)时,f′(x)>0,此时函数单调递增.因为f(0)=1>0,所以函数在(0,1)上没有零点.又f(-1)=1-1-
.当x∈(0,1)时,f′(x)>0,此时函数单调递增.当x∈(-1,0)时,f′(x)>0,此时函数单调递增.因为f(0)=1>0,所以函数在(0,1)上没有零点.又f(-1)=1-1-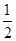 -
-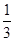 -…-
-…-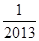 <0,所以函数在(-1,0)上有且只有一个零点,所以选C.
<0,所以函数在(-1,0)上有且只有一个零点,所以选C.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
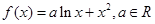
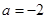 ,求证:函数
,求证:函数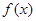 在(1,+∞)上是增函数;
在(1,+∞)上是增函数;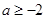 时,求函数
时,求函数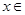 [l,e],使得
[l,e],使得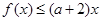 成立,求实数
成立,求实数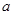 的取值范围.
的取值范围.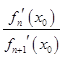 =
=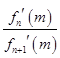 ,试比较x0与m的大小,并加以证明.
,试比较x0与m的大小,并加以证明.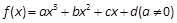 都有对称中心.请你探究函数
都有对称中心.请你探究函数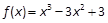 ,猜想它的对称中心为_________.
,猜想它的对称中心为_________.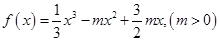 。
。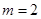 时,①求函数
时,①求函数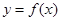 的单调区间;②求函数
的单调区间;②求函数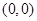 处的切线方程;
处的切线方程;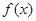 既有极大值,又有极小值,且当
既有极大值,又有极小值,且当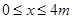 时,
时,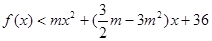 恒成立,求
恒成立,求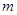 的取值范围.
的取值范围.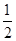 x-
x-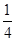 sinx-
sinx-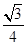 cosx的图象在点A(x0,y0)处的切线斜率为1,则tanx0=________.
cosx的图象在点A(x0,y0)处的切线斜率为1,则tanx0=________.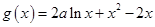 .
.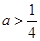 时,讨论函数
时,讨论函数 的单调性;
的单调性;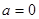 时,在函数
时,在函数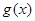 图象上取不同两点A、B,设线段AB的中点为
图象上取不同两点A、B,设线段AB的中点为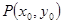 ,试探究函数
,试探究函数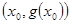 点处的切线与直线AB的位置关系?
点处的切线与直线AB的位置关系?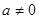 时
时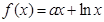 ,函数
,函数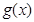 的导函数
的导函数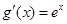 ,且
,且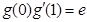 ,其中
,其中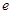 为自然对数的底数.
为自然对数的底数.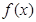 的极值;
的极值;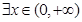 ,使得不等式
,使得不等式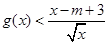 成立,试求实数
成立,试求实数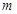 的取值范围;
的取值范围;