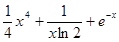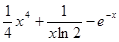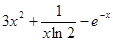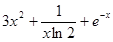题目内容
记函数fn(x)=a·xn-1(a∈R,n∈N*)的导函数为f′n(x),已知f′3(2)=12.
(1)求a的值;
(2)设函数gn(x)=fn(x)-n2ln x,试问:是否存在正整数n使得函数gn(x)有且只有一个零点?若存在,请求出所有n的值;若不存在,请说明理由;
(3)若实数x0和m(m>0且m≠1)满足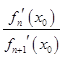 =
=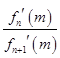 ,试比较x0与m的大小,并加以证明.
,试比较x0与m的大小,并加以证明.
(1)求a的值;
(2)设函数gn(x)=fn(x)-n2ln x,试问:是否存在正整数n使得函数gn(x)有且只有一个零点?若存在,请求出所有n的值;若不存在,请说明理由;
(3)若实数x0和m(m>0且m≠1)满足
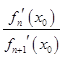 =
=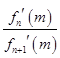 ,试比较x0与m的大小,并加以证明.
,试比较x0与m的大小,并加以证明.(1)a=1 (2)存在n=1,使得函数gn(x)有且只有一个零点.
(3)见解析
(3)见解析
解:(1)f3′(x)=3ax2,由f3′(2)=12得a=1.
(2)gn(x)=xn-n2ln x-1,
g′n(x)=nxn-1-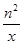 =
=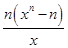 .
.
因为x>0,令gn′(x)=0得x=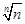 ,
,
当x>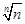 时,gn′(x)>0,gn(x)是增函数;
时,gn′(x)>0,gn(x)是增函数;
当0<x<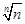 时,gn′(x)<0,gn(x)是减函数.
时,gn′(x)<0,gn(x)是减函数.
所以当x=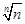 时,gn(x)有极小值,也是最小值,
时,gn(x)有极小值,也是最小值,
gn(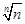 )=n-nln n-1.
)=n-nln n-1.
当x→0时,gn(x)→+∞;
当x→+∞时,gn(x)→+∞.
当n≥3时,gn(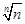 )=n(1-ln n)-1<0,函数gn(x)有两个零点;
)=n(1-ln n)-1<0,函数gn(x)有两个零点;
当n=2时,gn(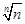 )=-2ln 2+1<0,函数gn(x)有两个零点;
)=-2ln 2+1<0,函数gn(x)有两个零点;
当n=1时,gn(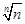 )=0,函数gn(x)有且只有一个零点.
)=0,函数gn(x)有且只有一个零点.
综上所述,存在n=1,使得函数gn(x)有且只有一个零点.
(3)fn′(x)=n·xn-1.
因为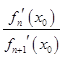 =
=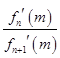 ,
,
所以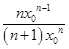 =
=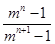 ,
,
解得x0=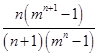 .
.
则x0-m=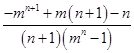 ,
,
当m>1时,(n+1)(mn-1)>0.
设h(x)=-xn+1+x(n+1)-n(x≥1),则h′(x)=-(n+1)xn+n+1=-(n+1)·(xn-1)≤0,当且仅当x=1时取等号,
所以h(x)在[1,+∞)上是减函数.
又m>1,所以h(m)<h(1)=0,
所以x0-m<0,所以x0<m.
当0<m<1时,(n+1)(mn-1)<0.
设h(x)=-xn+1+x(n+1)-n(0<x≤1),
则h′(x)=-(n+1)xn+n+1=-(n+1)·(xn-1)≥0,当且仅当x=1时取等号,所以h(x)在(0,1]上是增函数.
又因为0<m<1,所以h(m)<h(1)=0,
所以x0-m>0,所以x0>m.
综上所述,当m>1时,x0<m,当0<m<1时,x0>m.
(2)gn(x)=xn-n2ln x-1,
g′n(x)=nxn-1-
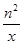 =
=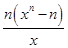 .
.因为x>0,令gn′(x)=0得x=
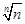 ,
,当x>
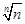 时,gn′(x)>0,gn(x)是增函数;
时,gn′(x)>0,gn(x)是增函数;当0<x<
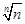 时,gn′(x)<0,gn(x)是减函数.
时,gn′(x)<0,gn(x)是减函数.所以当x=
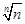 时,gn(x)有极小值,也是最小值,
时,gn(x)有极小值,也是最小值,gn(
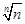 )=n-nln n-1.
)=n-nln n-1.当x→0时,gn(x)→+∞;
当x→+∞时,gn(x)→+∞.
当n≥3时,gn(
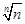 )=n(1-ln n)-1<0,函数gn(x)有两个零点;
)=n(1-ln n)-1<0,函数gn(x)有两个零点;当n=2时,gn(
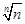 )=-2ln 2+1<0,函数gn(x)有两个零点;
)=-2ln 2+1<0,函数gn(x)有两个零点;当n=1时,gn(
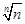 )=0,函数gn(x)有且只有一个零点.
)=0,函数gn(x)有且只有一个零点.综上所述,存在n=1,使得函数gn(x)有且只有一个零点.
(3)fn′(x)=n·xn-1.
因为
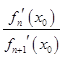 =
=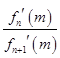 ,
,所以
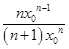 =
=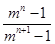 ,
,解得x0=
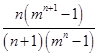 .
.则x0-m=
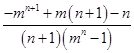 ,
,当m>1时,(n+1)(mn-1)>0.
设h(x)=-xn+1+x(n+1)-n(x≥1),则h′(x)=-(n+1)xn+n+1=-(n+1)·(xn-1)≤0,当且仅当x=1时取等号,
所以h(x)在[1,+∞)上是减函数.
又m>1,所以h(m)<h(1)=0,
所以x0-m<0,所以x0<m.
当0<m<1时,(n+1)(mn-1)<0.
设h(x)=-xn+1+x(n+1)-n(0<x≤1),
则h′(x)=-(n+1)xn+n+1=-(n+1)·(xn-1)≥0,当且仅当x=1时取等号,所以h(x)在(0,1]上是增函数.
又因为0<m<1,所以h(m)<h(1)=0,
所以x0-m>0,所以x0>m.
综上所述,当m>1时,x0<m,当0<m<1时,x0>m.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
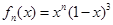 在
在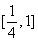 上的最大值为
上的最大值为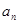 (
(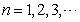 ).
).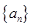 的通项公式;
的通项公式;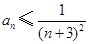 成立;
成立;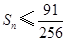 成立.
成立.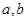 为常数,且
为常数,且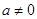 ,函数
,函数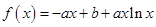 ,
,
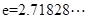 是自然对数的底数).
是自然对数的底数).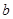 的值;
的值;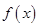 的单调区间;
的单调区间;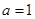 时,是否同时存在实数
时,是否同时存在实数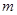 和
和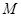 (
(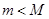 ),使得对每一个
),使得对每一个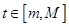 ,直线
,直线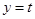 与曲线
与曲线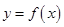
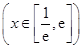 都有公共点?若存在,求出最小的实数
都有公共点?若存在,求出最小的实数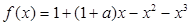 ,其中
,其中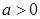 .
.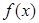 在其定义域上的单调性;
在其定义域上的单调性;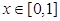 时,求
时,求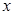 的值.
的值.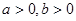 ,且函数
,且函数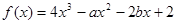 在
在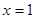 处有极值,则ab的最大值为 .
处有极值,则ab的最大值为 .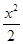 +
+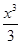 -
-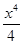 +…+
+…+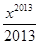 ,则下列结论正确的是( )
,则下列结论正确的是( )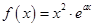 (
(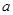 为小于
为小于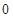 的常数).
的常数).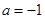 时,求函数
时,求函数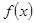 的单调区间;
的单调区间;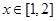 使不等式
使不等式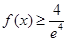 成立,求实数
成立,求实数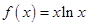 ,若
,若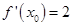 则
则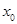 等于( )
等于( )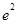
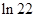
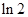
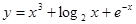 ,则
,则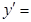 ( ).
( ).