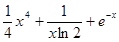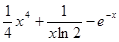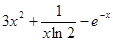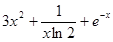题目内容
已知函数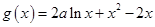 .
.
(1)当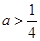 时,讨论函数
时,讨论函数 的单调性;
的单调性;
(2)当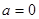 时,在函数
时,在函数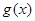 图象上取不同两点A、B,设线段AB的中点为
图象上取不同两点A、B,设线段AB的中点为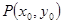 ,试探究函数
,试探究函数 在Q
在Q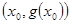 点处的切线与直线AB的位置关系?
点处的切线与直线AB的位置关系?
(3)试判断当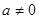 时
时 图象是否存在不同的两点A、B具有(2)问中所得出的结论.
图象是否存在不同的两点A、B具有(2)问中所得出的结论.
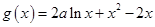 .
.(1)当
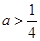 时,讨论函数
时,讨论函数 的单调性;
的单调性;(2)当
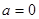 时,在函数
时,在函数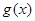 图象上取不同两点A、B,设线段AB的中点为
图象上取不同两点A、B,设线段AB的中点为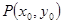 ,试探究函数
,试探究函数 在Q
在Q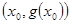 点处的切线与直线AB的位置关系?
点处的切线与直线AB的位置关系?(3)试判断当
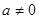 时
时 图象是否存在不同的两点A、B具有(2)问中所得出的结论.
图象是否存在不同的两点A、B具有(2)问中所得出的结论.(1)函数 在定义域
在定义域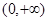 上单调递增;(2)函数在Q点处的切线与直线AB平行;
上单调递增;(2)函数在Q点处的切线与直线AB平行;
(3) 图象不存在不同的两点A、B具有(2)问中所得出的结论.
图象不存在不同的两点A、B具有(2)问中所得出的结论.
 在定义域
在定义域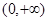 上单调递增;(2)函数在Q点处的切线与直线AB平行;
上单调递增;(2)函数在Q点处的切线与直线AB平行;(3)
 图象不存在不同的两点A、B具有(2)问中所得出的结论.
图象不存在不同的两点A、B具有(2)问中所得出的结论.试题分析:(1)求导即可知其单调性;(2)利用导数求出函数
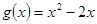 在点Q
在点Q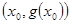 处的切线的斜率,再求出直线AB的斜率,可看出它们是相等的,所以函数在Q点处的切线与直线AB平行;
处的切线的斜率,再求出直线AB的斜率,可看出它们是相等的,所以函数在Q点处的切线与直线AB平行;(3)设
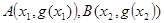
 ,若
,若 满足(2)中结论,则有
满足(2)中结论,则有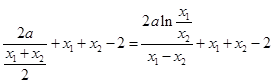 ,化简得
,化简得 (*).如果这个等式能够成立,则存在,如果这个等式不能成立,则不存在.设
(*).如果这个等式能够成立,则存在,如果这个等式不能成立,则不存在.设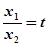 ,则*式整理得
,则*式整理得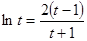 ,问题转化成该方程在
,问题转化成该方程在 上是否有解.再设函数
上是否有解.再设函数 ,下面通过导数即可知方程
,下面通过导数即可知方程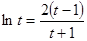 在
在 上是否有解,从而可确定函数
上是否有解,从而可确定函数 是否满足(2)中结论.
是否满足(2)中结论.(1)由题知
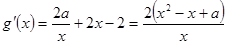 ,
,因为
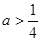 时,
时,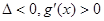 ,函数
,函数 在定义域
在定义域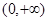 上单调递增; 4分
上单调递增; 4分(2)
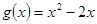 ,
, ,
,
所以函数Q点处的切线与直线AB平行; .7分
(3)设
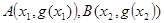
 ,若
,若 满足(2)中结论,有
满足(2)中结论,有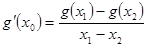 ,即
,即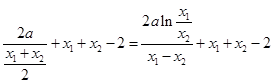
即
 (*) .9分
(*) .9分设
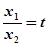 ,则*式整理得
,则*式整理得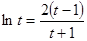 ,问题转化成该方程在
,问题转化成该方程在 上是否有解; 11分
上是否有解; 11分设函数
 ,则
,则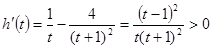 ,所以函数
,所以函数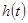 在
在 单调递增,即
单调递增,即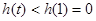 ,即方程
,即方程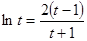 在
在 上无解,即函数
上无解,即函数 不满足(2)中结论. 14分
不满足(2)中结论. 14分
练习册系列答案
相关题目
 ,e])都有公共点?若存在,求出最小的实数m和最大的实数M;若不存在,说明理由.
,e])都有公共点?若存在,求出最小的实数m和最大的实数M;若不存在,说明理由. +
+ -
- +…+
+…+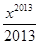 ,则下列结论正确的是( )
,则下列结论正确的是( )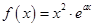 (
(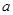 为小于
为小于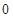 的常数).
的常数).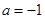 时,求函数
时,求函数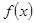 的单调区间;
的单调区间;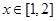 使不等式
使不等式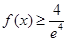 成立,求实数
成立,求实数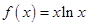 ,若
,若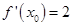 则
则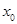 等于( )
等于( )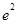
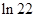
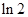
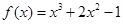 ,则
,则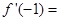 ( )
( )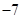



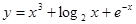 ,则
,则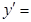 ( ).
( ).