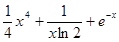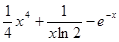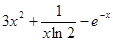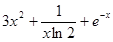题目内容
已知函数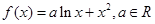
(1)若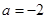 ,求证:函数
,求证:函数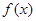 在(1,+∞)上是增函数;
在(1,+∞)上是增函数;
(2)当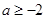 时,求函数
时,求函数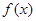 在[1,e]上的最小值及相应的x值;
在[1,e]上的最小值及相应的x值;
(3)若存在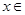 [l,e],使得
[l,e],使得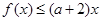 成立,求实数
成立,求实数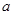 的取值范围.
的取值范围.
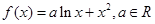
(1)若
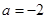 ,求证:函数
,求证:函数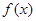 在(1,+∞)上是增函数;
在(1,+∞)上是增函数;(2)当
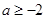 时,求函数
时,求函数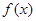 在[1,e]上的最小值及相应的x值;
在[1,e]上的最小值及相应的x值;(3)若存在
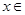 [l,e],使得
[l,e],使得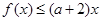 成立,求实数
成立,求实数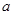 的取值范围.
的取值范围.(1)详见解析;(2) 的最小值为1,相应的x值为1;(3)
的最小值为1,相应的x值为1;(3)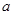 的取值范围是
的取值范围是 .
.
 的最小值为1,相应的x值为1;(3)
的最小值为1,相应的x值为1;(3)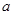 的取值范围是
的取值范围是 .
.试题分析:(1)当
 时,
时, ,当
,当 ,
, ,因此要证
,因此要证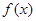 在
在 上是增函数,只需证明在
上是增函数,只需证明在 上有
上有 ,而这是显然成立的,故得证;(2)由(1)中的相关结论,可证当
,而这是显然成立的,故得证;(2)由(1)中的相关结论,可证当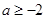 时,
时,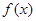 在
在 上是增函数,
上是增函数,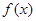 在
在 上的最小值即为
上的最小值即为
 ;(3)可将不等式
;(3)可将不等式 变形为
变形为 ,因此问题就等价于当
,因此问题就等价于当 时,
时,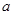 需满足
需满足 ,利用导数求函数
,利用导数求函数 在
在 上的单调性,可知
上的单调性,可知 在
在 上为增函数,故
上为增函数,故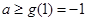 ,即
,即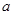 的取值范围是
的取值范围是 .
.(1)当
 时,
时, ,当
,当 ,
, ,
,故函数
 在
在 上是增函数 2分;
上是增函数 2分;(2)
 ,当
,当 ,
, ,
,当
 时,
时, 在
在 上非负(仅当
上非负(仅当 ,
, 时,
时, ),
),故函数
 在
在 上是增函数,此时
上是增函数,此时
 .
.∴当
 时,
时, 的最小值为1,相应的
的最小值为1,相应的 值为1. 5分;
值为1. 5分;(3)不等式
 ,可化为
,可化为 .
.∵
 , ∴
, ∴ 且等号不能同时取,所以
且等号不能同时取,所以 ,即
,即 ,
,因而
 (
( ),
),令
 (
( ),又
),又 ,
,当
 时,
时, ,
, ,
,从而
 (仅当x=1时取等号),所以
(仅当x=1时取等号),所以 在
在 上为增函数,
上为增函数,故
 的最小值为
的最小值为 ,所以
,所以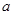 的取值范围是
的取值范围是 . 10分.
. 10分.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,e])都有公共点?若存在,求出最小的实数m和最大的实数M;若不存在,说明理由.
,e])都有公共点?若存在,求出最小的实数m和最大的实数M;若不存在,说明理由.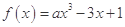 对于
对于 总有
总有
 0 成立,则
0 成立,则 = .
= .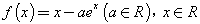 .已知函数
.已知函数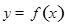 有两个零点
有两个零点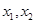 ,且
,且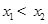 .
.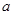 的取值范围;
的取值范围;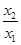 随着
随着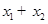 随着
随着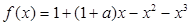 ,其中
,其中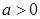 .
.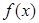 在其定义域上的单调性;
在其定义域上的单调性;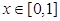 时,求
时,求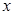 的值.
的值.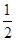 .
.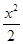 +
+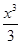 -
-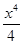 +…+
+…+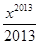 ,则下列结论正确的是( )
,则下列结论正确的是( )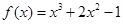 ,则
,则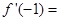 ( )
( )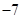



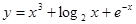 ,则
,则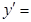 ( ).
( ).