题目内容
7.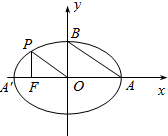 如图,A,A′,B分别是椭圆顶点,从椭圆上一点P向x轴作垂线,垂足为左焦点F,且AB∥OP,则椭圆的离心率为$\frac{\sqrt{2}}{2}$.
如图,A,A′,B分别是椭圆顶点,从椭圆上一点P向x轴作垂线,垂足为左焦点F,且AB∥OP,则椭圆的离心率为$\frac{\sqrt{2}}{2}$.
分析 先计算PF1的长,再利用两直线平行得tan∠POF1,最后在直角三角形POF1中,找到a、b、c间的等式,从而求出离心率
解答 解:设F1(-c,0),将x=-c代入$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$,得y=±$\frac{{b}^{2}}{a}$
∴PF1=$\frac{{b}^{2}}{a}$,OF1=c
∵AB∥OP,∴tan∠POF1=tan∠BAO=$\frac{b}{a}$
∴在直角三角形POF1中,tan∠POF1=$\frac{{PF}_{1}}{{OF}_{1}}$=$\frac{{b}^{2}}{ac}$=$\frac{b}{a}$
∴b=c,∴a=$\sqrt{2}$c
∴e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$.
故答案为:$\frac{\sqrt{2}}{2}$.
点评 本题考查了椭圆的几何性质,椭圆离心率的求法,将已知几何条件转化为椭圆特征量a、b、c间的关系,是解决本题的关键.

练习册系列答案
相关题目
17.一个不透明圆锥体的正视图和侧视图(左视图)为两全等的正三角形,若将它倒立放在桌面上(即圆锥体的顶点在桌面上),则该圆锥体在桌面上从垂直位置旋转到水平位置的过程中,其在水平桌面上正投影不可能是( )
| A. |  圆形区域 | |
| B. | 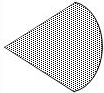 等腰三角形两腰与半椭圆围成的区域 | |
| C. | 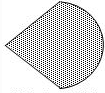 等腰三角形两腰与半圆围成的区域 | |
| D. |  椭圆形区域 |
15.已知函数f(x)=a-x2(1≤x≤2)与g(x)=x+1的图象上存在关于x轴对称的点,则实数a的取值范围是( )
| A. | $[-\frac{5}{4},+∞)$ | B. | [1,2] | C. | $[-\frac{5}{4},1]$ | D. | [-1,1] |
12.袋中有10个外形相同的球,其中5个白球,3个黑球,2个红球,从中任意取出一球,已知它不是白球,则它是黑球的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{5}$ |
16.下列各组函数中,表示同一函数的是( )
| A. | $y=x+1与y=\frac{{{x^2}+x}}{x}$ | B. | $f(x)=\frac{x^2}{{{{({\sqrt{x}})}^2}}}与g(x)=x$ | ||
| C. | $f(x)=x\frac{|x|}{x}与f(t)=\left\{\begin{array}{l}t(t>0)\\-t(t<0)\end{array}\right.$ | D. | $f(x)=|x|与g(x)=\left\{\begin{array}{l}x(x>0)\\-x(x<0)\end{array}\right.$ |
17.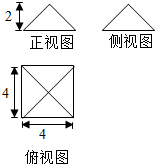 图为某个几何体的三视图,则该几何体的表面积为( )
图为某个几何体的三视图,则该几何体的表面积为( )
 图为某个几何体的三视图,则该几何体的表面积为( )
图为某个几何体的三视图,则该几何体的表面积为( )| A. | 32 | B. | 16+16$\sqrt{2}$ | C. | 48 | D. | 16+32$\sqrt{2}$ |
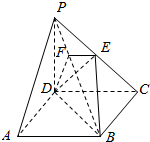 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=1,点E是PC的中点,作EF⊥PB交PB于点F.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=1,点E是PC的中点,作EF⊥PB交PB于点F.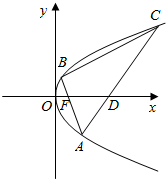 已知抛物线T:y2=2px(p>0)的焦点为F,A(x0,y0)为T上异于原点的任意一点,点D为x的正半轴上的点,且有|FA|=|FD|,若x0=3时,D的横坐标为5.
已知抛物线T:y2=2px(p>0)的焦点为F,A(x0,y0)为T上异于原点的任意一点,点D为x的正半轴上的点,且有|FA|=|FD|,若x0=3时,D的横坐标为5.