题目内容
16．下列各组函数中，表示同一函数的是（ ）| A． | $y=x+1与y=\frac{{{x^2}+x}}{x}$ | B． | $f（x）=\frac{x^2}{{{{（{\sqrt{x}}）}^2}}}与g（x）=x$ | ||
| C． | $f（x）=x\frac{|x|}{x}与f（t）=\left\{\begin{array}{l}t（t＞0）\\-t（t＜0）\end{array}\right.$ | D． | $f（x）=|x|与g（x）=\left\{\begin{array}{l}x（x＞0）\\-x（x＜0）\end{array}\right.$ |
分析 判断函数的定义域以及对应法则是否相同，推出结果即可．
解答 解：$y=x+1与y=\frac{{x}^{2}+x}{x}$，两个函数的定义域不相同，所以不是相同函数．
$f（x）=\frac{{x}^{2}}{{（\sqrt{x}）}^{2}}与g（x）=x$，两个函数的定义域不相同，所以不是相同函数．
$f（x）=x\frac{|x|}{x}=\left\{\begin{array}{l}x（x＞0）\\-x（x＜0）\end{array}\right.与f（t）=\left\{\begin{array}{l}t（t＞0）\\-t（t＜0）\end{array}\right.$，两个函数的定义域相同，对应法则相同，所以是相同函数．
$f（x）=|x|与g（x）=\left\{\begin{array}{l}x（x＞0）\\-x（x＜0）\end{array}\right.$，两个函数的定义域不相同，所以不是相同函数．
故选：C．
点评 本题考查函数的定义的应用，是基本知识的考查．
练习册系列答案
相关题目
6．已知函数f（x）=$\sqrt{3}$sinωx+cosωx（其中ω＞0）的图象与x轴交点的横坐标构成一个公差为$\frac{π}{2}$的等差数列，把函数f（x）的图象沿x轴向左平移$\frac{π}{6}$个单位得到函数g（x）的图象，则g（x）的单调递减区间是（ ）
| A． | [kπ，$\frac{π}{2}$+kπ]，k∈Z | B． | [-$\frac{π}{2}$+kπ，kπ]，k∈Z | ||
| C． | [-$\frac{π}{4}$+kπ，$\frac{π}{4}$+kπ]，k∈Z | D． | [$\frac{π}{4}$+kπ，$\frac{3π}{4}$+kπ]，k∈Z |
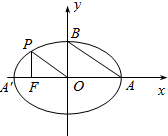如图，A，A′，B分别是椭圆顶点，从椭圆上一点P向x轴作垂线，垂足为左焦点F，且AB∥OP，则椭圆的离心率为$\frac{\sqrt{2}}{2}$．