题目内容
17.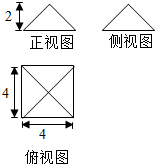 图为某个几何体的三视图,则该几何体的表面积为( )
图为某个几何体的三视图,则该几何体的表面积为( )| A. | 32 | B. | 16+16$\sqrt{2}$ | C. | 48 | D. | 16+32$\sqrt{2}$ |
分析 根据几何体的三视图,得出该几何体是正四棱锥,结合图中数据,即可求出它的表面积.
解答 解:根据几何体的三视图,得;
该几何体是底面边长为4,高为2的正四棱锥,
所以该四棱锥的斜高为$\sqrt{{2}^{2}{+2}^{2}}$=2$\sqrt{2}$;
所以该四棱锥的侧面积为
4×$\frac{1}{2}$×4×2$\sqrt{2}$=16$\sqrt{2}$,
底面积为4×4=16,
所以几何体的表面积为16+16$\sqrt{2}$.
故选:B.
点评 本题考查了利用空间几何体的三视图求表面积的应用问题,是基础题目.

练习册系列答案
相关题目
8.设变量x,y满足$\left\{\begin{array}{l}x-y+1≥0\\ x+y-3≥0\\ 2x-y-3≤0\end{array}\right.$则目标函数z=2x+3y的最大值为( )
| A. | 7 | B. | 8 | C. | 22 | D. | 23 |
12.焦点为(0,±3),且与双曲线$\frac{x^2}{2}-{y^2}=1$有相同的渐近线的双曲线方程是( )
| A. | $\frac{x^2}{3}-\frac{y^2}{6}=1$ | B. | $\frac{y^2}{3}-\frac{x^2}{6}=1$ | C. | $\frac{y^2}{6}-\frac{x^2}{3}=1$ | D. | $\frac{x^2}{6}-\frac{y^2}{3}=1$ |
2.若f:A→B能构成映射,把集合A中的元素叫原像,在集合B中与A中的元素相对应的元素叫像.下列说法正确的有( )
(1)A中的任一元素在B中必须有像且唯一; (2)B中的元素可以在A中无原像;
(3)B中的多个元素可以在A中有相同的原像;(4)像的集合就是集合B.
(1)A中的任一元素在B中必须有像且唯一; (2)B中的元素可以在A中无原像;
(3)B中的多个元素可以在A中有相同的原像;(4)像的集合就是集合B.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.已知一条直线与一个平面内的两条直线垂直.则该直线与这个平面的位置关系为( )
| A. | 平行 | B. | 相交 | C. | 在平面内 | D. | 都有可能 |
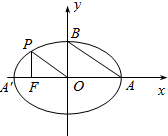 如图,A,A′,B分别是椭圆顶点,从椭圆上一点P向x轴作垂线,垂足为左焦点F,且AB∥OP,则椭圆的离心率为$\frac{\sqrt{2}}{2}$.
如图,A,A′,B分别是椭圆顶点,从椭圆上一点P向x轴作垂线,垂足为左焦点F,且AB∥OP,则椭圆的离心率为$\frac{\sqrt{2}}{2}$.