题目内容
已知首项为 的等比数列
的等比数列 不是递减数列,其前n项和为
不是递减数列,其前n项和为 ,且
,且 成等差数列。
成等差数列。
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的最大项的值与最小项的值。
的最大项的值与最小项的值。
 的等比数列
的等比数列 不是递减数列,其前n项和为
不是递减数列,其前n项和为 ,且
,且 成等差数列。
成等差数列。(1)求数列
 的通项公式;
的通项公式;(2)设
 ,求数列
,求数列 的最大项的值与最小项的值。
的最大项的值与最小项的值。(1)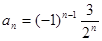 (2)
(2)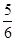 ,
,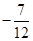
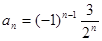 (2)
(2)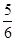 ,
,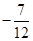
试题分析:
(1)根据
 成等差数列,利用等比数列通项公式和前
成等差数列,利用等比数列通项公式和前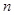 项和公式,展开.利用等比数列
项和公式,展开.利用等比数列 不是递减数列,可得
不是递减数列,可得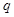 值,进而求通项.
值,进而求通项.(2)首先根据(1)得到
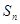 ,进而得到
,进而得到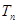 ,但是等比数列的公比是负数,所以分两种情况:当的当n为奇数时,
,但是等比数列的公比是负数,所以分两种情况:当的当n为奇数时, 随n的增大而减小,所以
随n的增大而减小,所以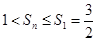 ;当n为偶数时,
;当n为偶数时, 随n的增大而增大,所以
随n的增大而增大,所以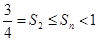 ,然后可判断最值.
,然后可判断最值.试题解析:
(1)设
 的公比为q。由
的公比为q。由 成等差数列,得
成等差数列,得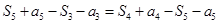 .
.即
 ,则
,则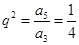 .
.又
 不是递减数列且
不是递减数列且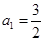 ,所以
,所以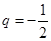 .
.故
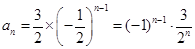 .
.(2)由(1)利用等比数列的前
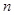 项和公式,可得得
项和公式,可得得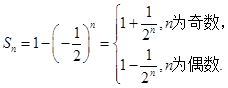
当n为奇数时,
 随n的增大而减小,所以
随n的增大而减小,所以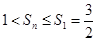 ,
,故
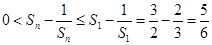 .
.当n为偶数时,
 随n的增大而增大,所以
随n的增大而增大,所以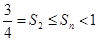 ,
,故
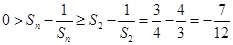 .
. 综上,对于
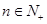 ,总有
,总有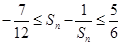 ,
,所以数列
 最大项的值为
最大项的值为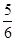 ,最小值的值为
,最小值的值为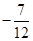 .
.
练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 的前
的前 项和为
项和为 .已知
.已知 ,
, =an+1-
=an+1- n2-n-
n2-n- (
( )
) 的值;
的值; +
+ +…+
+…+ <
< .
.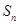 是它的前n项和.若S16>0,且
是它的前n项和.若S16>0,且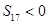 ,则当
,则当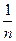 sin
sin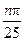 ,
,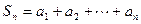 ,在
,在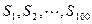 中,正数的个数是( )
中,正数的个数是( ) 的前n项和为
的前n项和为 ,若
,若 ,则
,则 =__________。
=__________。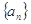 和
和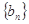 的通项公式分别为
的通项公式分别为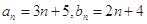 ,则它们的公共项按从小到大的顺序组成的新数列
,则它们的公共项按从小到大的顺序组成的新数列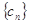 的通项公式为___________.
的通项公式为___________.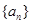 中,
中,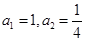 ,若
,若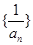 为等差数列,则数列
为等差数列,则数列
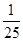
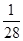
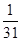
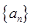 的前
的前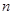 项和为
项和为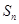 ,若
,若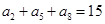 ,则
,则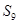 等于( )
等于( )


