题目内容
已知函数f (x)=asinx+btanx+1,满足f (5)=7,则f (-5)的值为( )
| A、5 | B、-5 | C、6 | D、-6 |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:利用函数奇偶性特征,求出f(-x)+f(x)的值,再利用f(5)的值求出f(-5)的值,得到本题结论.
解答:
解:∵函数f(x)=asinx+btanx+1,
∴f(-x)=asin(-x)+btan(-x)+1=-asinx-btanx+1,
∴f(-x)+f(x)=2,
∴f(-5)+f(5)=2.
∵f(5)=7,
∴f(-5)=-5.
故选B.
∴f(-x)=asin(-x)+btan(-x)+1=-asinx-btanx+1,
∴f(-x)+f(x)=2,
∴f(-5)+f(5)=2.
∵f(5)=7,
∴f(-5)=-5.
故选B.
点评:本题考查了函数的奇偶性,本题难度不大,属于基础题.

练习册系列答案
相关题目
已知
=(0,1,1),
=(-2,2,0),则向量
与
的夹角为( )
| a |
| b |
| a |
| b |
| A、30° | B、45° |
| C、60° | D、90° |
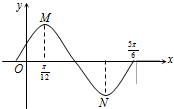 如图是函数y=Asin(ωx+φ)(A>0,ω>0|φ|<
如图是函数y=Asin(ωx+φ)(A>0,ω>0|φ|<